Thanks very much for pointing out. I have updated.

Statistical modeling, partial pooling, Multilevel modeling, hierarchical modeling

Pricing is a common problem faced by any e-commerce business, and one that can be addressed effectively by Bayesian statistical methods.

The Mercari Price Suggestion data set from Kaggle seems to be a good candidate for the Bayesian models I wanted to learn.

If you remember, the purpose of the data set is to build a model that automatically suggests the right price for any given product for Mercari website sellers. I am here to attempt to see whether we can solve this problem by Bayesian statistical methods, using PyStan.

And the following pricing analysis replicates the case study of home radon levels from Professor Fonnesbeck. In fact, the methodology and code were largely borrowed from his tutorial.

The Data

In this analysis, we will estimate parameters for individual product price that exist within categories. And the measured price is a function of the shipping condition (buyer pays shipping or seller pays shipping), and the overall price.

At the end, our estimate of the parameter of product price can be considered a prediction.

Simply put, the independent variables we are using are: category_name & shipping. And the dependent variable is: price.

from scipy import stats
import arviz as az
import numpy as np
import matplotlib.pyplot as plt
import pystan
import seaborn as sns
import pandas as pd
from theano import shared
from sklearn import preprocessing
plt.style.use('bmh')

df = pd.read_csv('train.tsv', sep = 't')
df = df.sample(frac=0.01, random_state=99)
df = df[pd.notnull(df['category_name'])]

df.category_name.nunique()

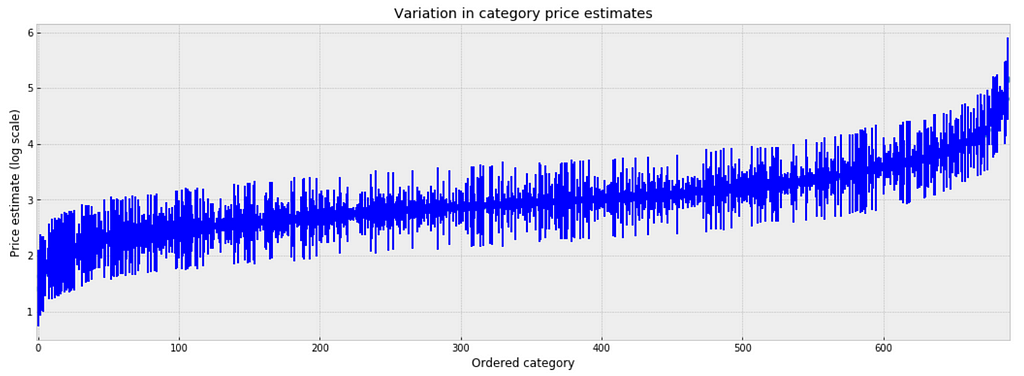
To make things more interesting, I will model all of these 689 product categories. If you want to produce better results quicker, you may want to model the top 10 or top 20 categories, to start.

shipping_0 = df.loc[df['shipping'] == 0, 'price']
shipping_1 = df.loc[df['shipping'] == 1, 'price']
fig, ax = plt.subplots(figsize=(10,5))
ax.hist(shipping_0, color='#8CB4E1', alpha=1.0, bins=50, range = [0, 100],
       label=0)
ax.hist(shipping_1, color='#007D00', alpha=0.7, bins=50, range = [0, 100],
       label=1)
plt.xlabel('price', fontsize=12)
plt.ylabel('frequency', fontsize=12)
plt.title('Price Distribution by Shipping Type', fontsize=15)
plt.tick_params(labelsize=12)
plt.legend()
plt.show();

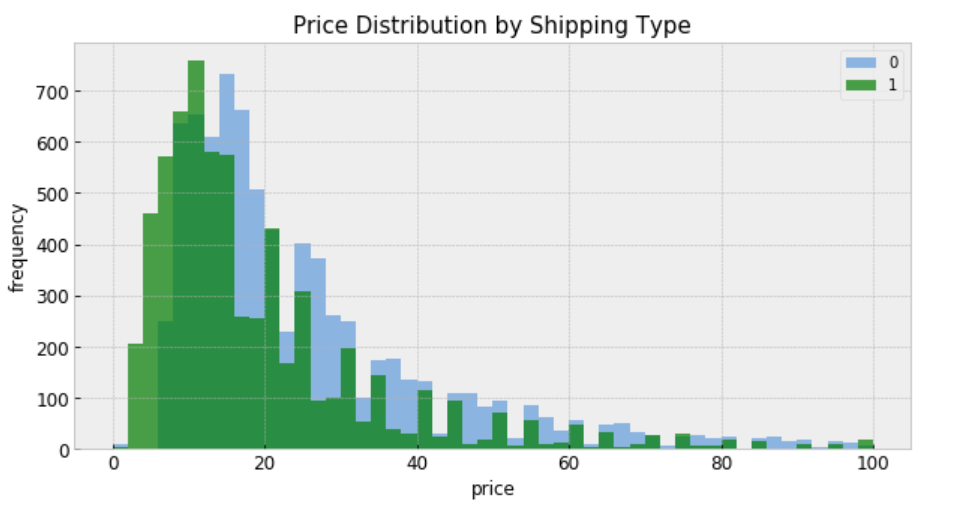
“shipping = 0” means shipping fee paid by buyer, and “shipping = 1” means shipping fee paid by seller. In general, price is higher when buyer pays shipping.

Modeling

For construction of a Stan model, it is convenient to have the relevant variables as local copies — this aids readability.

• category: index code for each category name
• price: price
• category_names: unique category names
• categories: number of categories
• log_price: log price
• shipping: who pays shipping
• category_lookup: index categories with a lookup dictionary

le = preprocessing.LabelEncoder()
df['category_code'] = le.fit_transform(df['category_name'])
category_names = df.category_name.unique()
categories = len(category_names)
category = df['category_code'].values
price = df.price
df['log_price'] = log_price = np.log(price + 0.1).values
shipping = df.shipping.values
category_lookup = dict(zip(category_names, range(len(category_names))))

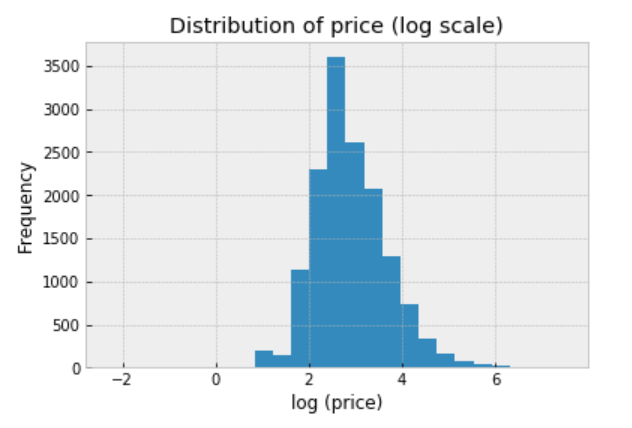
We should always explore the distribution of price (log scale) in the data:

df.price.apply(lambda x: np.log(x+0.1)).hist(bins=25)
plt.title('Distribution of price (log scale)')
plt.xlabel('log (price)')
plt.ylabel('Frequency');

Conventional Approaches

There are two conventional approaches to modeling price represent the two extremes of the bias-variance tradeoff:

Complete pooling:

Treat all categories the same, and estimate a single price level, with the equation:

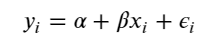
To specify this model in Stan, we begin by constructing the data block, which includes vectors of log-price measurements (y) and who pays shipping covariates (x), as well as the number of samples (N).

The complete pooling model is:

https://medium.com/media/51a3101eb6118ee17ae87ea25bc4edb0/href

When passing the code, data, and parameters to the Stan function, we specify sampling 2 chains of length 1000:

https://medium.com/media/c57be4f2144e862403f9dc722036fd0e/href

Inspecting the fit

Once the fit has been run, the method extract and specifying permuted=True extracts samples into a dictionary of arrays so that we can conduct visualization and summarization.

We are interested in the mean values of these estimates for parameters from the sample.

• b0 = alpha = mean price across category
• m0 = beta = mean variation in price with change on who pays shipping

We can now visualize how well this pooled model fits the observed data.

pooled_sample = pooled_fit.extract(permuted=True)
b0, m0 = pooled_sample['beta'].T.mean(1)

plt.scatter(df.shipping, np.log(df.price+0.1))
xvals = np.linspace(-0.2, 1.2)
plt.xticks([0, 1])
plt.plot(xvals, m0*xvals+b0, 'r--')
plt.title("Fitted model")
plt.xlabel("Shipping")
plt.ylabel("log(price)");

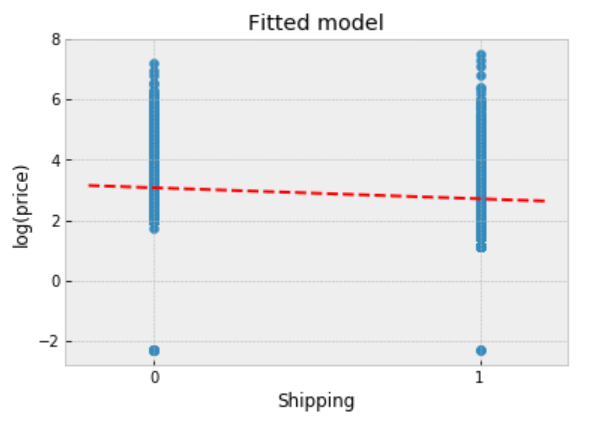
Observations:

• The fitted line runs through the centre of the data, and it describes the trend.
• However, the observed points vary widely about the fitted model, and there are multiple outliers indicating that the original price varies quite widely.
• We might expect different gradients if we chose different subsets of the data.

Unpooling

When unpooling, we model price in each category independently, with the equation:

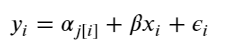
where j = 1, … , 689

The unpooled model is:

https://medium.com/media/17665e2ecce7247121bde96788c0f169/href

When running the unpooled model in Stan, We again map Python variables to those used in the Stan model, then pass the data, parameters and the model to Stan. We again specify 1000 iterations of 2 chains.

https://medium.com/media/0255b96493f2197f098e598785e6bb50/href

Inspecting the fit

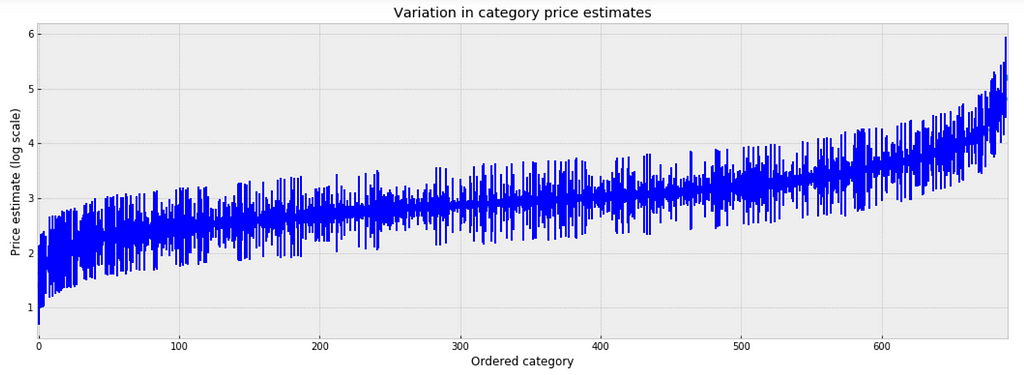
To inspect the variation in predicted price at category level, we plot the mean of each estimate with its associated standard error. To structure this visually, we’ll reorder the categories such that we plot categories from the lowest to the highest.

unpooled_estimates = pd.Series(unpooled_fit['a'].mean(0), index=category_names)

order = unpooled_estimates.sort_values().index

plt.figure(figsize=(18, 6))
plt.scatter(range(len(unpooled_estimates)), unpooled_estimates[order])
for i, m, se in zip(range(len(unpooled_estimates)), unpooled_estimates[order], unpooled_se[order]):
    plt.plot([i,i], [m-se, m+se], 'b-') 
    plt.xlim(-1,690); 
plt.ylabel('Price estimate (log scale)');plt.xlabel('Ordered category');plt.title('Variation in category price estimates');

Observations:

• There are multiple categories with relatively low predicted price levels, and multiple categories with a relatively high predicted price levels. Their distance can be large.
• A single all-category estimate of all price level could not represent this variation well.

Comparison of pooled and unpooled estimates

We can make direct visual comparisons between pooled and unpooled estimates for all categories, and we are going to show several examples, and I purposely select some categories with many products, and other categories with very few products.

https://medium.com/media/2470950a8e5c243beeb1acebee519701/href

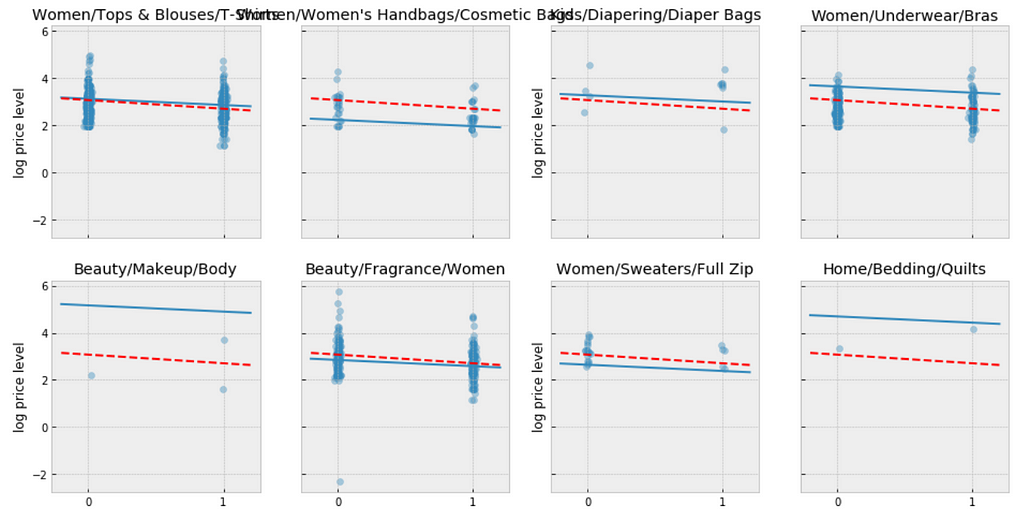
Let me try to explain what the above visualizations tell us:

• The pooled models (red dashed line) in every category are the same, meaning all categories are modeled the same, indicating pooling is useless.
• For categories with few observations, the fitted estimates track the observations very closely, suggesting that there has been overfitting. So that we can’t trust the estimates produced by models using few observations.

Multilevel and Hierarchical Models

Partial Pooling — simplest

The simplest possible partial pooling model for the e-commerce price data set is one that simply estimates prices, with no other predictors (i.e. ignoring the effect of shipping). This is a compromise between pooled (mean of all categories) and unpooled (category-level means), and approximates a weighted average (by sample size) of unpooled category estimates, and the pooled estimates, with the equation:

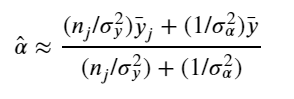
The simplest partial pooling model:

https://medium.com/media/66824a405e17c27e56dcb4bb92ff8830/href

Now we have two standard deviations, one describing the residual error of the observations, and another describing the variability of the category means around the average.

https://medium.com/media/73b49d1cd60ce693f146761352779f89/href

We’re interested primarily in the category-level estimates of price, so we obtain the sample estimates for “a”:

https://medium.com/media/e17f1f478ee3f3b2d6785917db1e316b/href

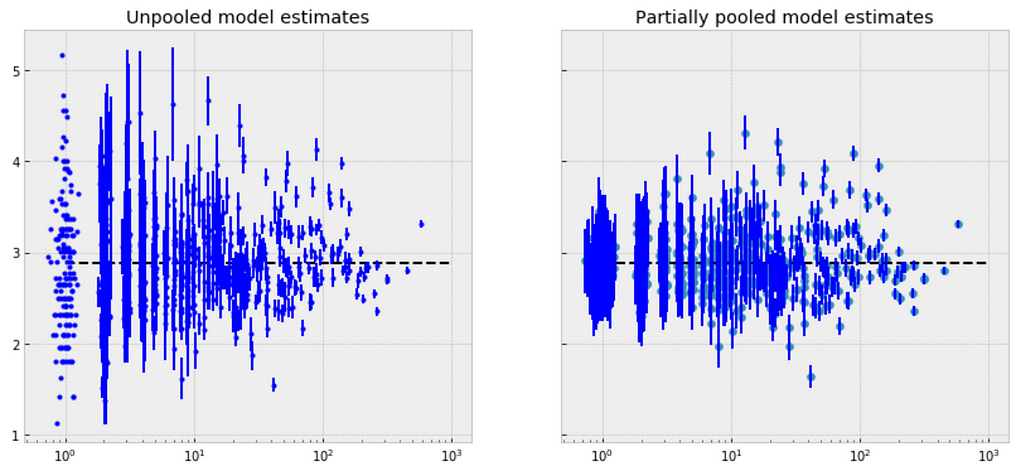
Observations:

• There are significant differences between unpooled and partially-pooled estimates of category-level price, The partially pooled estimates looks way less extreme.

Partial Pooling — Varying Intercept

Simply put, the multilevel modeling shares strength among categories, allowing for more reasonable inference in categories with little data, with the equation:

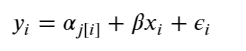
The varying intercept model:

https://medium.com/media/7e6b2af5c74e7d7e9ee8c34e0135ff2e/href

Fitting the model:

https://medium.com/media/b1ba4fcf65194d4cc1eebad8a1dddd0a/href

There is no way to visualize all of these 689 categories together, so I will visualize 20 of them.

a_sample = pd.DataFrame(varying_intercept_fit['a'])
plt.figure(figsize=(20, 5))
g = sns.boxplot(data=a_sample.iloc[:,0:20], whis=np.inf, color="g")
# g.set_xticklabels(df.category_name.unique(), rotation=90)  # label counties
g.set_title("Estimates of log(price), by category")
g;

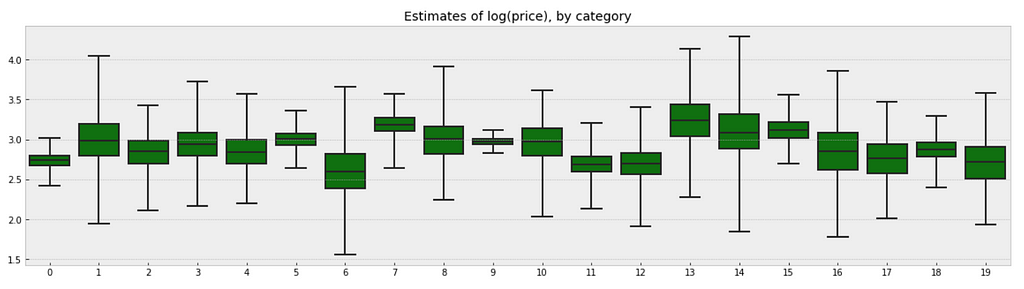
Observations:

• There are quite some variations in prices by category, and we can see that for example, category Beauty/Fragrance/Women (index at 9) with a large number of samples (225) also has one of the tightest range of estimated values.
• While category Beauty/Hair Care/Shampoo Plus Conditioner (index at 16) with the smallest number of sample (one only) also has one of the widest range of estimates.

We can visualize the distribution of parameter estimates for 𝜎 and β.

az.plot_trace(varying_intercept_fit, var_names = ['sigma_a', 'b']);

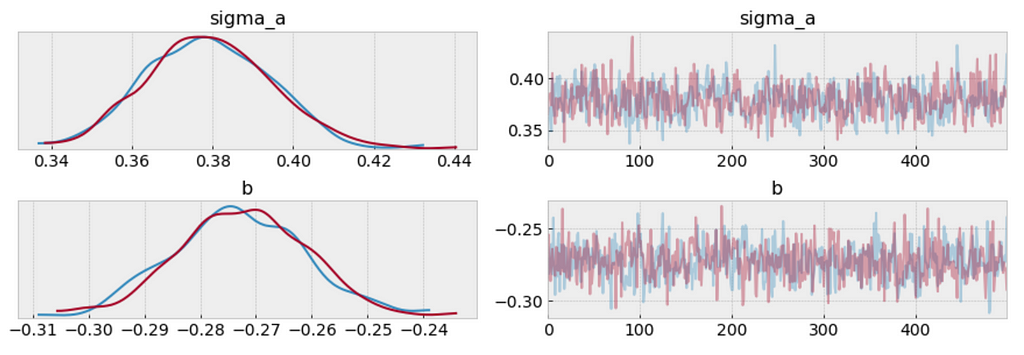
varying_intercept_fit['b'].mean()

The estimate for the shipping coefficient is approximately -0.27, which can be interpreted as products which shipping fee paid by seller at about 0.76 of (exp(−0.27)=0.76) the price of those shipping paid by buyer, after accounting for category.

Visualize the fitted model

plt.figure(figsize=(12, 6))
xvals = np.arange(2)
bp = varying_intercept_fit['a'].mean(axis=0) # mean a (intercept) by category
mp = varying_intercept_fit['b'].mean()      # mean b (slope/shipping effect)
for bi in bp:
    plt.plot(xvals, mp*xvals + bi, 'bo-', alpha=0.4)
plt.xlim(-0.1,1.1)
plt.xticks([0, 1])
plt.title('Fitted relationships by category')
plt.xlabel("shipping")
plt.ylabel("log(price)");

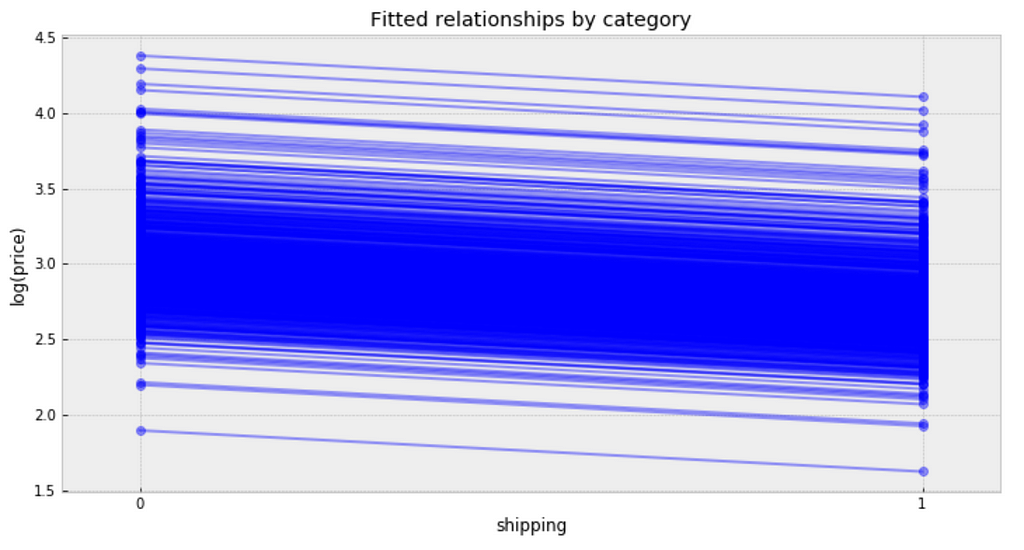
Observations:

• It is clear from this plot that we have fitted the same shipping effect to each category, but with a different price level in each category.
• There is one category with very low fitted price estimates, and several categories with relative lower fitted price estimates.
• There are multiple categories with relative higher fitted price estimates.
• The bulk of categories form a majority set of similar fits.

We can see whether partial pooling of category-level price estimate has provided more reasonable estimates than pooled or unpooled models, for categories with small sample sizes.

Partial Pooling — Varying Slope model

We can also build a model that allows the categories to vary according to shipping arrangement (paid by buyer or paid by seller) influences the price. With the equation:

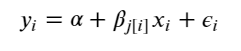
The varying slope model:

https://medium.com/media/410f626d1b3edc5f64a95b8d5d6c5875/href

Fitting the model:

https://medium.com/media/c46f1284c4d604f1a809af03d0920c50/href

Following the process earlier, we will visualize 20 categories.

b_sample = pd.DataFrame(varying_slope_fit['b'])
plt.figure(figsize=(20, 5))
g = sns.boxplot(data=b_sample.iloc[:,0:20], whis=np.inf, color="g")
# g.set_xticklabels(df.category_name.unique(), rotation=90)  # label counties
g.set_title("Estimate of shipping effect, by category")
g;

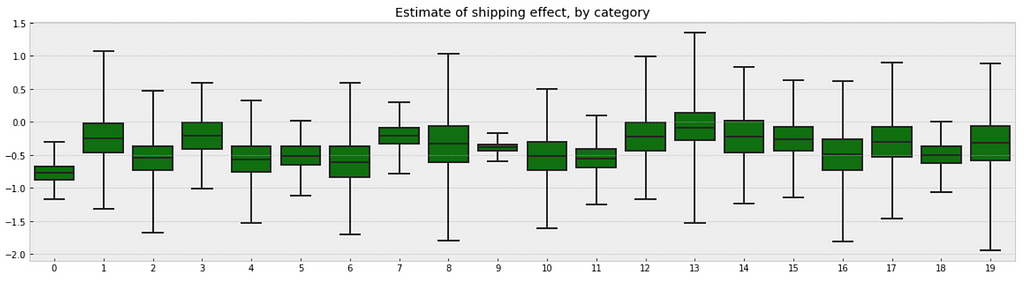
Observations:

• From the first glance, we may not see any difference between these two boxplots. But if you look deeper, you will find that the variation in median estimates between categories in varying slope model becomes smaller than those in varying intercept model, though the range of uncertainty is still greatest in the categories with fewest products, and least in the categories with the most products.

Visualize the fitted model:

plt.figure(figsize=(10, 6))
xvals = np.arange(2)
b = varying_slope_fit['a'].mean()
m = varying_slope_fit['b'].mean(axis=0)
for mi in m:
    plt.plot(xvals, mi*xvals + b, 'bo-', alpha=0.4)
plt.xlim(-0.2, 1.2)
plt.xticks([0, 1])
plt.title("Fitted relationships by category")
plt.xlabel("shipping")
plt.ylabel("log(price)");

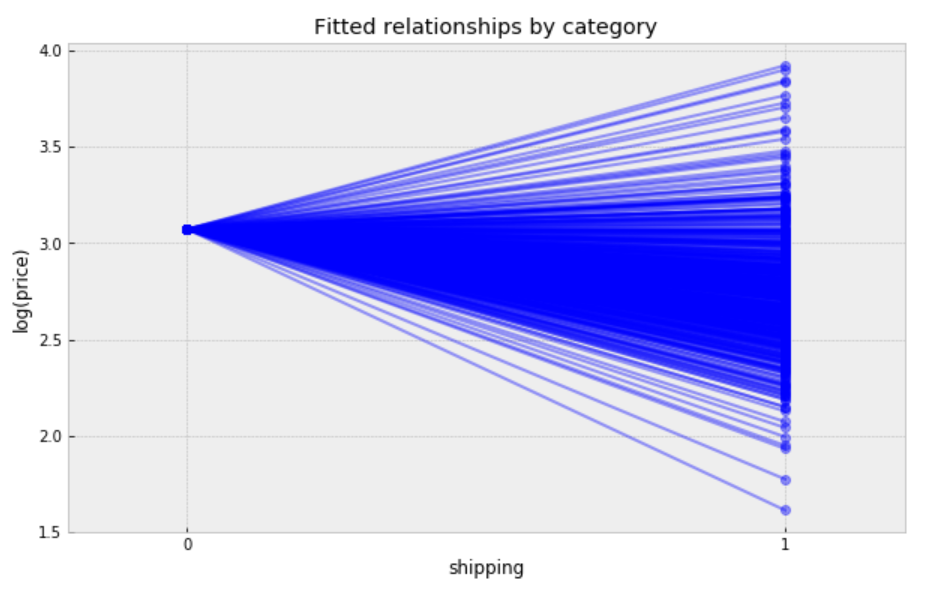
Observations:

• It is clear from this plot that we have fitted the same price level to every category, but with a different shipping effect in each category.
• There are two categories with very small shipping effects, but the majority bulk of categories form a majority set of similar fits.

Partial Pooling — Varying Slope and Intercept

The most general way to allow both slope and intercept to vary by category. With the equation:

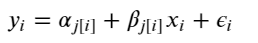
The varying slope and intercept model:

https://medium.com/media/99f0024765a13153517815289c68ed0f/href

Fitting the model:

https://medium.com/media/2b2e35474baef1997aa31d66cf469bb7/href

Visualize the fitted model:

plt.figure(figsize=(10, 6))
xvals = np.arange(2)
b = varying_intercept_slope_fit['a'].mean(axis=0)
m = varying_intercept_slope_fit['b'].mean(axis=0)
for bi,mi in zip(b,m):
    plt.plot(xvals, mi*xvals + bi, 'bo-', alpha=0.4)
plt.xlim(-0.1, 1.1);
plt.xticks([0, 1])
plt.title("fitted relationships by category")
plt.xlabel("shipping")
plt.ylabel("log(price)");

While these relationships are all very similar, we can see that by allowing both shipping effect and price to vary, we seem to be capturing more of the natural variation, compare with varying intercept model.

Contextual Effects

In some instances, having predictors at multiple levels can reveal correlation between individual-level variables and group residuals. We can account for this by including the average of the individual predictors as a covariate in the model for the group intercept.

Contextual effect model:

https://medium.com/media/7c604f58453416f772d0c991ee56a12d/href

Fitting the model:

https://medium.com/media/6b84784f1d5a7f049d18afc5e84f18dd/href

Prediction

we wanted to make a prediction for a new product in “Women/Athletic Apparel/Pants, Tights, Leggings” category, which shipping paid by seller, we just need to sample from the model with the appropriate intercept.

category_lookup['Women/Athletic Apparel/Pants, Tights, Leggings']

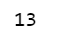
The prediction model:

https://medium.com/media/a65424df0289f71c90c9e6bf88374c61/href

Making the prediction:

https://medium.com/media/7e5baafd8775536b65d5be80b0650606/href

The prediction:

contextual_pred_fit.plot('y_wa');

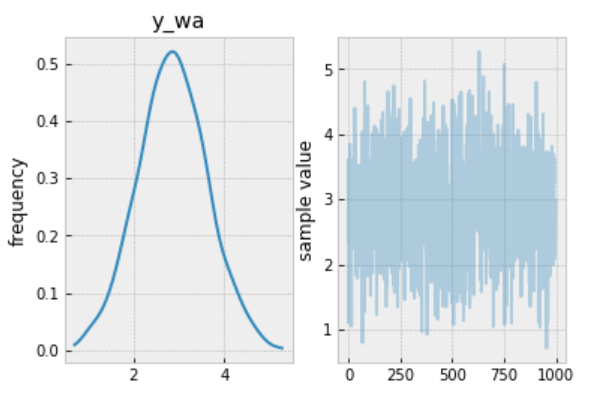
Observations:

• The mean value sampled from this fit is ≈3, so we should expect the measured price in a new product in “Women/Athletic Apparel/Pants, Tights, Leggings” category, when shipping paid by seller, to be ≈exp(3) ≈ 20.09, though the range of predicted values is rather wide.

Jupyter notebook can be found on Github. Enjoy the rest of the weekend.

References:

• Multilevel Modeling
• widdowquinn/Teaching-Stan-Hierarchical-Modelling

Student’s t-distribution, Poisson distribution, Negative Binomial distribution, Hierarchical modeling and Regression

Twitter conducted a study recently in the US, found that customers were willing to pay nearly $20 more to travel with an airline that had responded to their tweet in under six minutes. When they got a response over 67 minutes after their tweet, they would only pay $2 more to fly with that airline.

When I came across Customer Support on Twitter dataset, I couldn’t help but wanted to model and compare airlines customer service twitter response time.

I wanted to be able to answer questions like:

• Are there significant differences on customer service twitter response time among all the airlines in the data?
• Is the weekend affect response time?
• Do longer tweets take longer time to respond?
• Which airline has the shortest customer service twitter response time and vice versa?

The data

It is a large dataset contains hundreds of companies from all kinds of industries. The following data wrangling process will accomplish:

• Get customer inquiry, and corresponding response from the company in every row.
• Convert datetime columns to datetime data type.
• Calculate response time to minutes.
• Select only airline companies in the data.
• Any customer inquiry that takes longer than 60 minutes will be filtered out. We are working on requests that get response in 60 minutes.
• Create time attributes and response word count.

https://medium.com/media/9d8cc66aa77dae417cd2246b510ddf2b/href

Response time distribution

plt.figure(figsize=(10,5))
sns.distplot(df['response_time'], kde=False)
plt.title('Frequency of response by response time')
plt.xlabel('Response time (minutes)')
plt.ylabel('Number of responses');

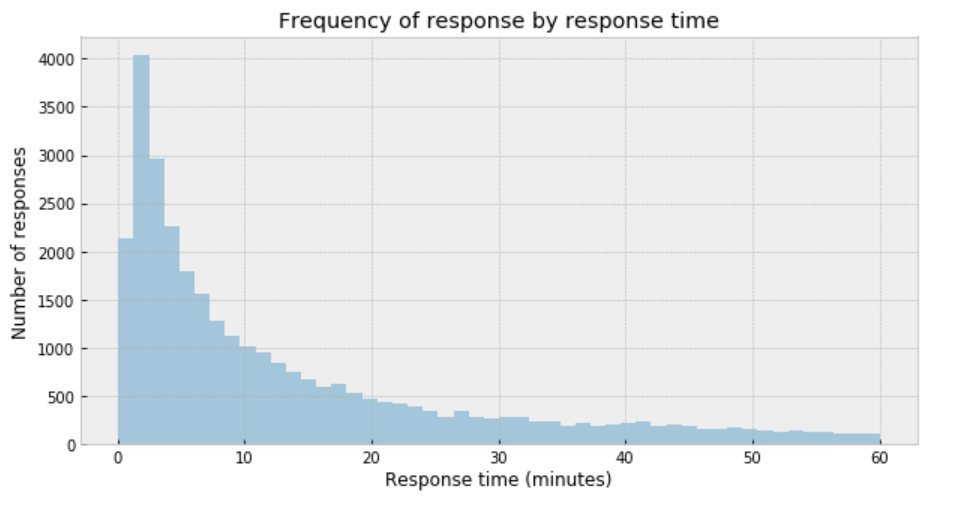
My immediate impression is that a Gaussian distribution is not a proper description of the data.

Student’s t-distribution

One useful option when dealing with outliers and Gaussian distributions is to replace the Gaussian likelihood with a Student’s t-distribution. This distribution has three parameters: the mean (𝜇), the scale (𝜎) (analogous to the standard deviation), and the degrees of freedom (𝜈).

• Set the boundaries of the uniform distribution of the mean to be 0 and 60.
• 𝜎 can only be positive, therefore use HalfNormal distribution.
• set 𝜈 as an exponential distribution with a mean of 1.

https://medium.com/media/c927243a9e1b9abe286dc505c48653d1/href

MCMC diagnostics

• From the following trace plot, we can visually get the plausible values of 𝜇 from the posterior.
• We should compare this result with those from the the result we obtained analytically.

az.plot_trace(trace_t[:1000], var_names = ['μ']);

df.response_time.mean()

• The left plot shows the distribution of values collected for 𝜇. What we get is a measure of uncertainty and credible values of 𝜇 between 7.4 and 7.8 minutes.
• It is obvious that samples that have been drawn from distributions that are significantly different from the target distribution.

Posterior predictive check

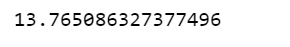
One way to visualize is to look if the model can reproduce the patterns observed in the real data. For example, how close are the inferred means to the actual sample mean:

ppc = pm.sample_posterior_predictive(trace_t, samples=1000, model=model_t)
_, ax = plt.subplots(figsize=(10, 5))
ax.hist([n.mean() for n in ppc['y']], bins=19, alpha=0.5)
ax.axvline(df['response_time'].mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');

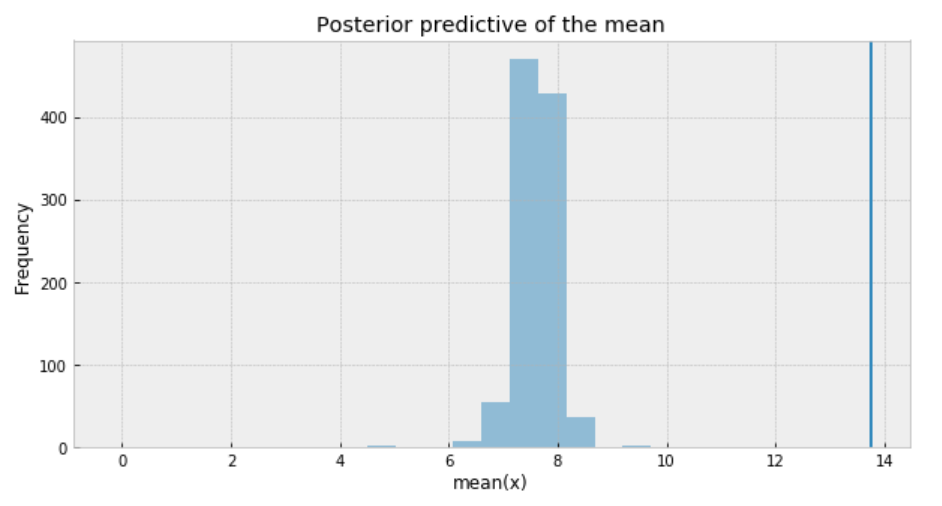
The inferred mean is so far away from the actual sample mean. This confirms that Student’s t-distribution is not a proper choice for our data.

Poisson distribution

Poisson distribution is generally used to describe the probability of a given number of events occurring on a fixed time/space interval. Thus, the Poisson distribution assumes that the events occur independently of each other and at a fixed interval of time and/or space. This discrete distribution is parametrized using only one value 𝜇, which corresponds to the mean and also the variance of the distribution.

https://medium.com/media/88200a01173117a5fe4003d8ceeb2f0b/href

MCMC diagnostics

az.plot_trace(trace_p);

The measure of uncertainty and credible values of 𝜇 is between 13.22 and 13.34 minutes. It sounds way better already.

Autocorrelations

We want the autocorrelation drops with increasing x-axis in the plot. Because this indicates a low degree of correlation between our samples.

_ = pm.autocorrplot(trace_p, var_names=['μ'])

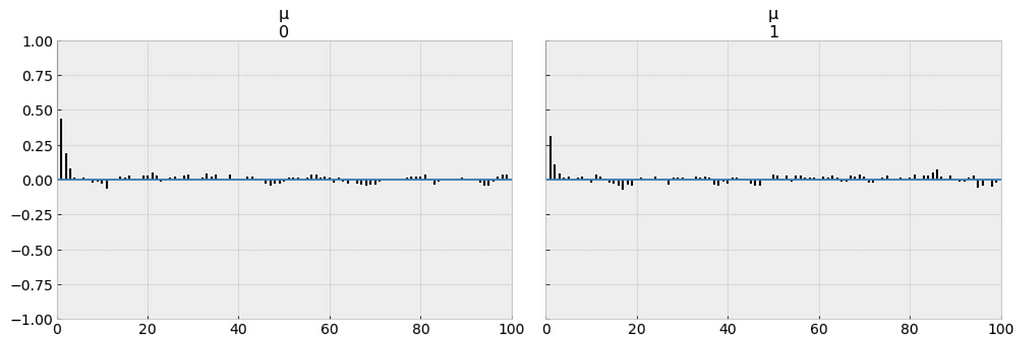
Our samples from the Poisson model has dropped to low values of autocorrelation, which is a good sign.

Posterior predictive check

We use posterior predictive check to “look for systematic discrepancies between real and simulated data”. There are multiple ways to do posterior predictive check, and I’d like to check if my model makes sense in various ways.

y_ppc_p = pm.sample_posterior_predictive(
    trace_p, 100, model_p, random_seed=123)
y_pred_p = az.from_pymc3(trace=trace_p, posterior_predictive=y_ppc_p)
az.plot_ppc(y_pred_p, figsize=(10, 5), mean=False)
plt.xlim(0, 60);

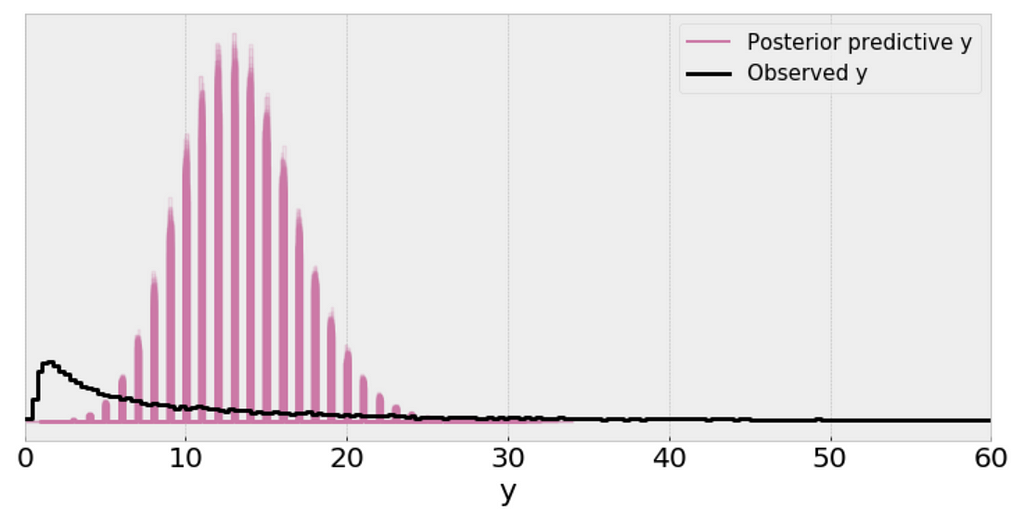
Interpretation:

• The single (black) line is a kernel density estimate (KDE) of the data and the many purple lines are KDEs computed from each one of the 100 posterior predictive samples. The purple lines reflect the uncertainty we have about the inferred distribution of the predicted data.
• From the above plot, I can’t consider the scale of a Poisson distribution as a reasonable practical proxy for the standard deviation of the data even after removing outliers.

Posterior predictive check

ppc = pm.sample_posterior_predictive(trace_p, samples=1000, model=model_p)
_, ax = plt.subplots(figsize=(10, 5))
ax.hist([n.mean() for n in ppc['y']], bins=19, alpha=0.5)
ax.axvline(df['response_time'].mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');

• The inferred means to the actual sample mean are much closer than what we got from Student’s t-distribution. But still, there is a small gap.
• The problem with using a Poisson distribution is that mean and variance are described by the same parameter. So one way to solve this problem is to model the data as a mixture of Poisson distribution with rates coming from a gamma distribution, which gives us the rationale to use the negative-binomial distribution.

Negative binomial distribution

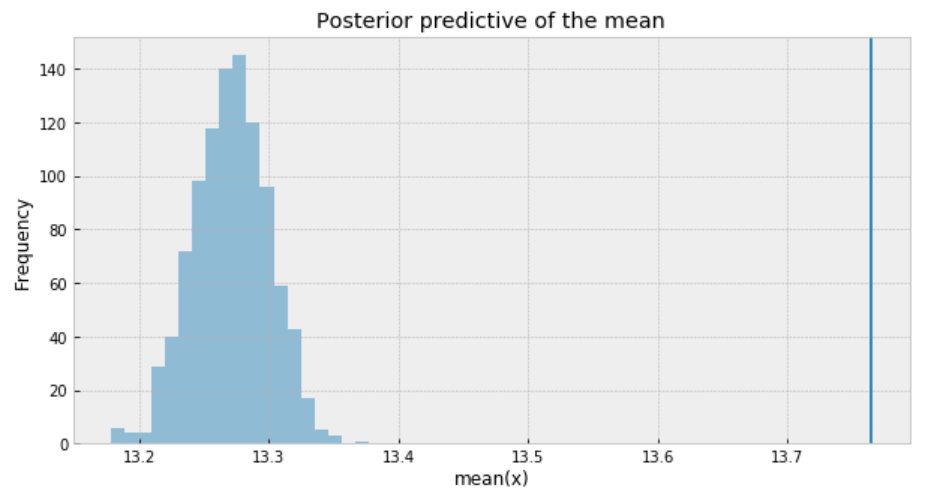
Negative binomial distribution has very similar characteristics to the Poisson distribution except that it has two parameters (𝜇 and 𝛼) which enables it to vary its variance independently of its mean.

https://medium.com/media/5979510cd27f69dc726e5eeba9574b01/href

MCMC diagnostics

az.plot_trace(trace_n, var_names=['μ', 'α']);

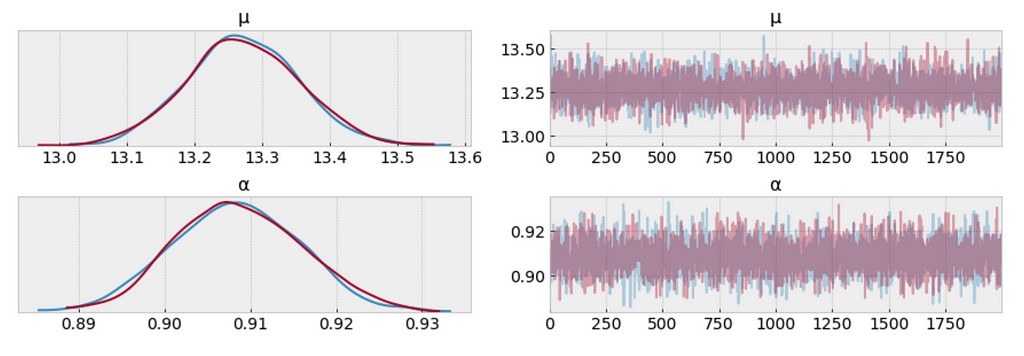
The measure of uncertainty and credible values of 𝜇 is between 13.0 and 13.6 minutes, and it is very closer to the target sample mean.

Posterior predictive check

y_ppc_n = pm.sample_posterior_predictive(
    trace_n, 100, model_n, random_seed=123)
y_pred_n = az.from_pymc3(trace=trace_n, posterior_predictive=y_ppc_n)
az.plot_ppc(y_pred_n, figsize=(10, 5), mean=False)
plt.xlim(0, 60);

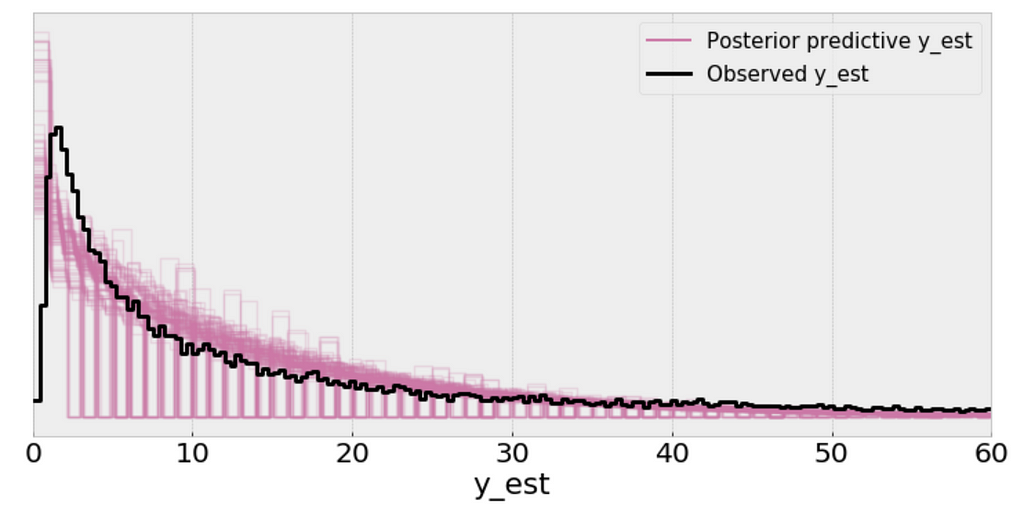
Using the Negative binomial distribution in our model leads to predictive samples that seem to better fit the data in terms of the location of the peak of the distribution and also its spread.

Posterior predictive check

ppc = pm.sample_posterior_predictive(trace_n, samples=1000, model=model_n)
_, ax = plt.subplots(figsize=(10, 5))
ax.hist([n.mean() for n in ppc['y_est']], bins=19, alpha=0.5)
ax.axvline(df['response_time'].mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');

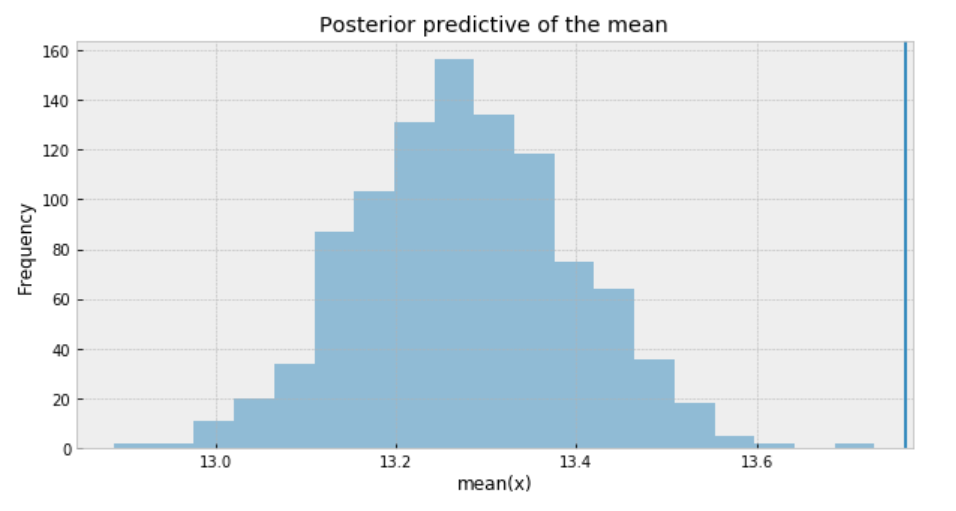
To sum it up, the following are what we get for the measure of uncertainty and credible values of (𝜇):

• Student t-distribution: 7.4 to 7.8 minutes
• Poisson distribution: 13.22 to 13.34 minutes
• Negative Binomial distribution: 13.0 to 13.6 minutes.

Posterior predictive distribution

https://medium.com/media/30e11e4826d9d4b8cc3d54e91077daec/href

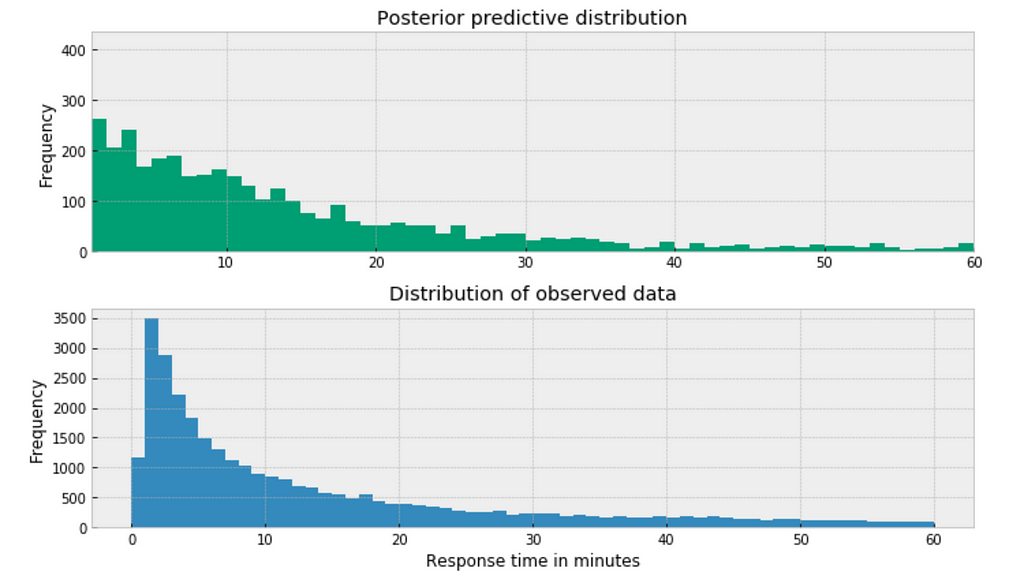
The posterior predictive distribution somewhat resembles the distribution of the observed data, suggesting that the Negative binomial model is a more appropriate fit for the underlying data.

Bayesian methods for hierarchical modeling

• We want to study each airline as a separated entity. We want to build a model to estimate the response time of each airline and, at the same time, estimate the response time of the entire data. This type of model is known as a hierarchical model or multilevel model.
• My intuition would suggest that different airline has different response time. The customer service twitter response from AlaskaAir might be faster than the response from AirAsia for example. As such, I decide to model each airline independently, estimating parameters μ and α for each airline.
• One consideration is that some airlines may have fewer customer inquiries from twitter than others. As such, our estimates of response time for airlines with few customer inquires will have a higher degree of uncertainty than airlines with a large number of customer inquiries. The below plot illustrates the discrepancy in sample size per airline.

plt.figure(figsize=(12,4))
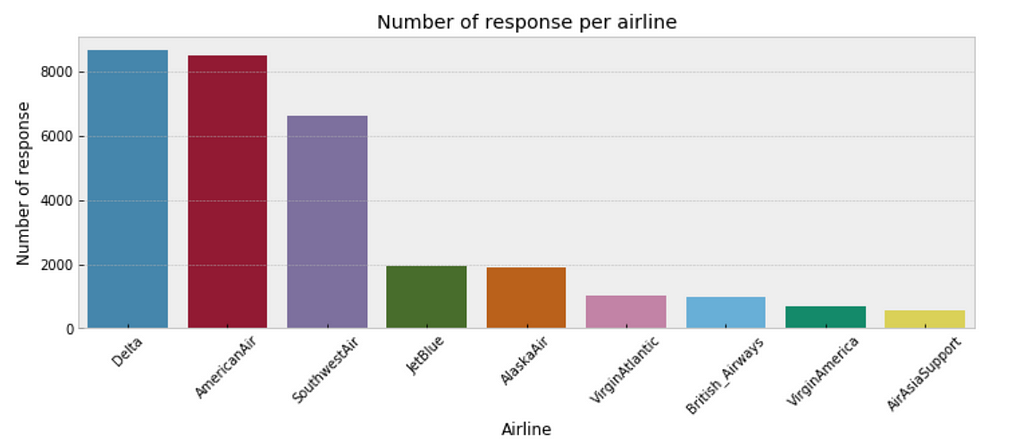
sns.countplot(x="author_id_y", data=df, order = df['author_id_y'].value_counts().index)
plt.xlabel('Airline')
plt.ylabel('Number of response')
plt.title('Number of response per airline')
plt.xticks(rotation=45);

Bayesian modeling each airline with negative binomial distribution

https://medium.com/media/4cdc4a72b3aede34b23dbb275d318aa4/href

Posterior predictive distribution for each airline

https://medium.com/media/139d5455997414082cd04ff48a930649/href

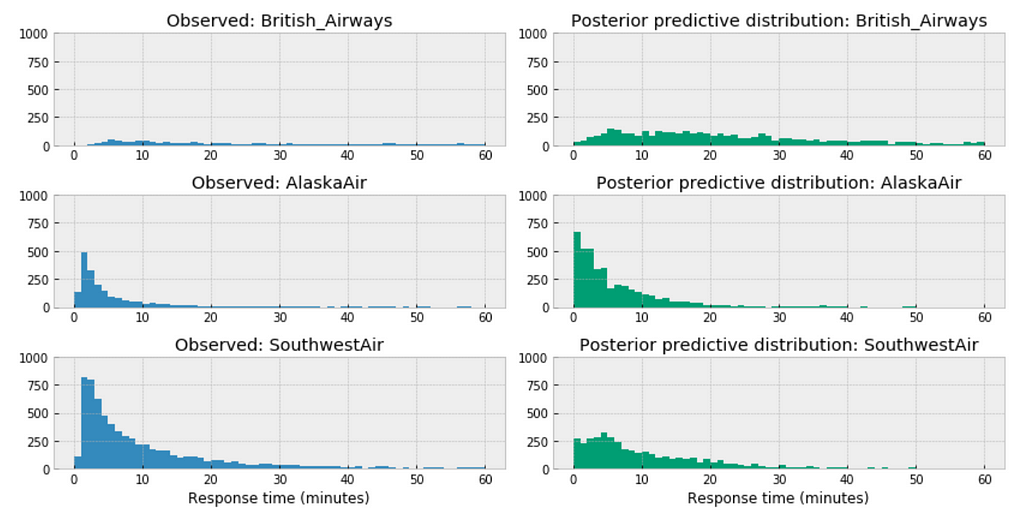
Observations:

• Among the above three airlines, British Airways’ posterior predictive distribution vary considerably to AlaskaAir and SouthwestAir. The distribution of British Airways towards right.
• This could accurately reflect the characteristics of its customer service twitter response time, means in general it takes longer for British Airways to respond than those of AlaskaAir or SouthwestAir.
• Or it could be incomplete due to small sample size, as we have way more data from Southwest than from British airways.

https://medium.com/media/a44e953f4ed2177f1b19ba489bcb0bc7/href

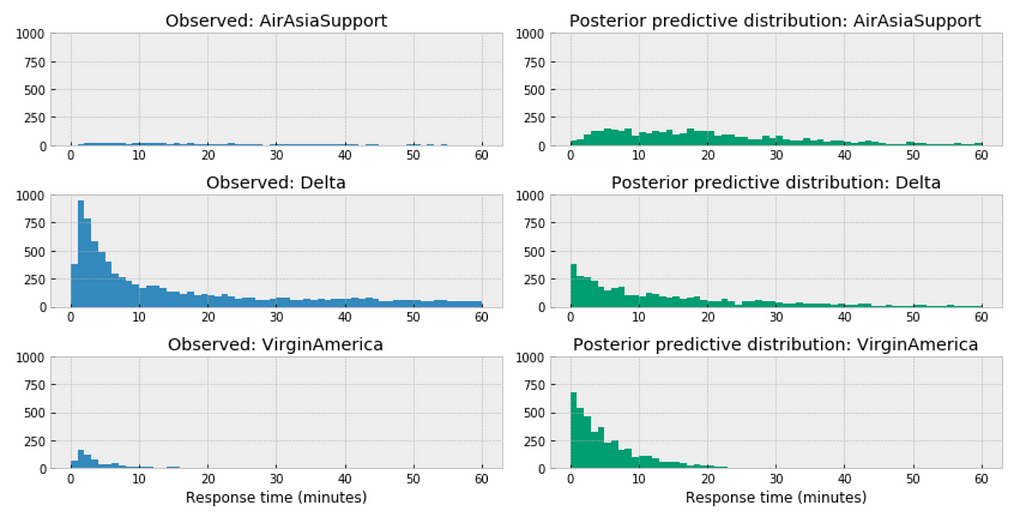
Similar here, among the above three airlines, the distribution of AirAsia towards right, this could accurately reflect the characteristics of its customer service twitter response time, means in general, it takes longer for AirAsia to respond than those of Delta or VirginAmerica. Or it could be incomplete due to small sample size.

https://medium.com/media/0c0a9ee55f4bd298907e0d10f79f1f71/href

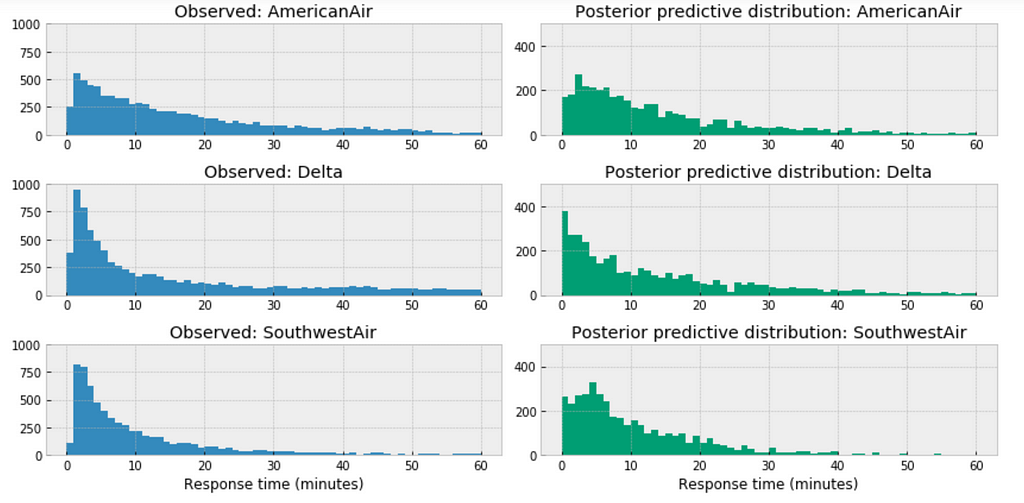
For the airlines we have relative sufficient data, for example, when we compare the above three large airlines in the United States, the posterior predictive distribution do not seem to vary significantly.

Bayesian Hierarchical Regression

The variables for the model:

df = df[['response_time', 'author_id_y', 'created_at_y_is_weekend', 'word_count']]
formula = 'response_time ~ ' + ' + '.join(['%s' % variable for variable in df.columns[1:]])
formula

In the following code snippet, we:

• Convert categorical variables to integer.
• Estimate a baseline parameter value 𝛽0 for each airline customer service response time.
• Estimate all the other parameter across the entire population of the airlines in the data.

https://medium.com/media/3076b071ea036ac663f5e91609ca1cb3/href

MCMC diagnostics

az.plot_trace(trace_hr);

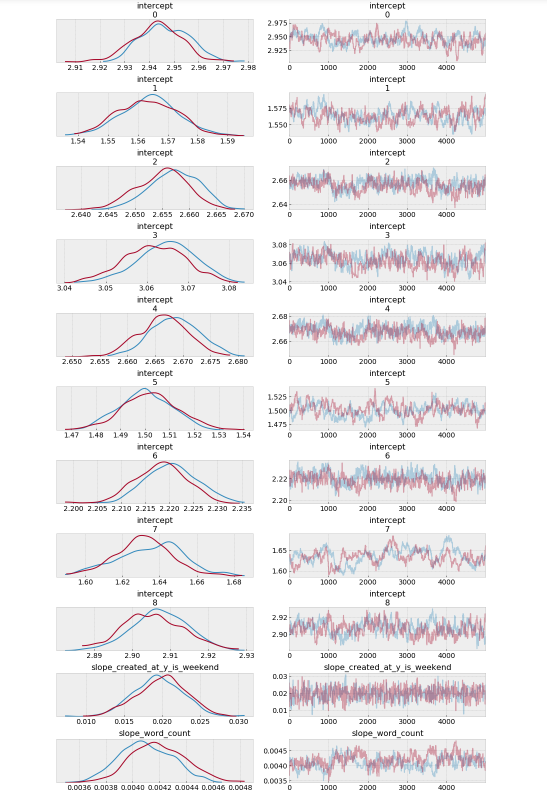
Observations:

• Each airline has a different baseline response time, however, several of them are pretty close.
• If you send a request over the weekend, you would expect a marginally longer wait time before getting a response.
• The more words on the response, the marginally longer wait time before getting a response.

Forest plot

_, ax = pm.forestplot(trace_hr, var_names=['intercept'])
ax[0].set_yticklabels(airlines.tolist());

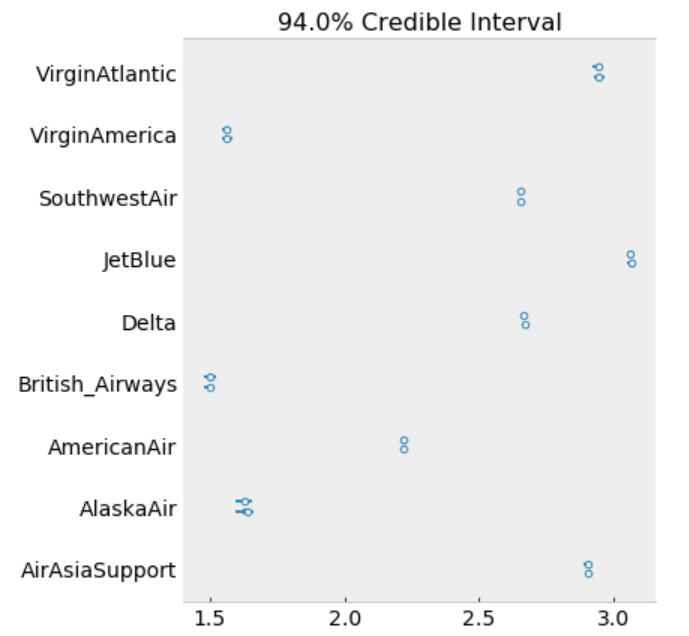
The model estimates the above β0 (intercept) parameters for every airline. The dot is the most likely value of the parameter for each airline. It look like our model has very little uncertainty for every airline.

ppc = pm.sample_posterior_predictive(trace_hr, samples=2000, model=model_hr)
az.r2_score(df.response_time.values, ppc['y_est'])

Jupyter notebook can be located on the Github. Have a productive week!

References:

The book: Bayesian Analysis with Python

The book: Doing Bayesian Data Analysis

The book: Statistical Rethinking

https://docs.pymc.io/notebooks/GLM-poisson-regression.html

https://docs.pymc.io/notebooks/hierarchical_partial_pooling.html

GLM: Hierarchical Linear Regression – PyMC3 3.6 documentation

https://docs.pymc.io/notebooks/GLM-negative-binomial-regression.html

• Notebook on nbviewer
• PyMC3 and Theano – PyMC3 3.6 documentation

https://www.kaggle.com/psbots/customer-support-meets-spacy-universe

Bayesian Modeling Airlines Customer Service Twitter Response Time was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Thanks for letting me know.

I have loaded a small set here: https://raw.githubusercontent.com/susanli2016/Machine-Learning-with-Python/master/data/renfe_small.csv

Feel free to use it.

That part shouldn’t be there. I have updated Github. Thanks for letting me know.

How likely am I to subscribe a term deposit? Posterior probability, credible interval, odds ratio, WAIC

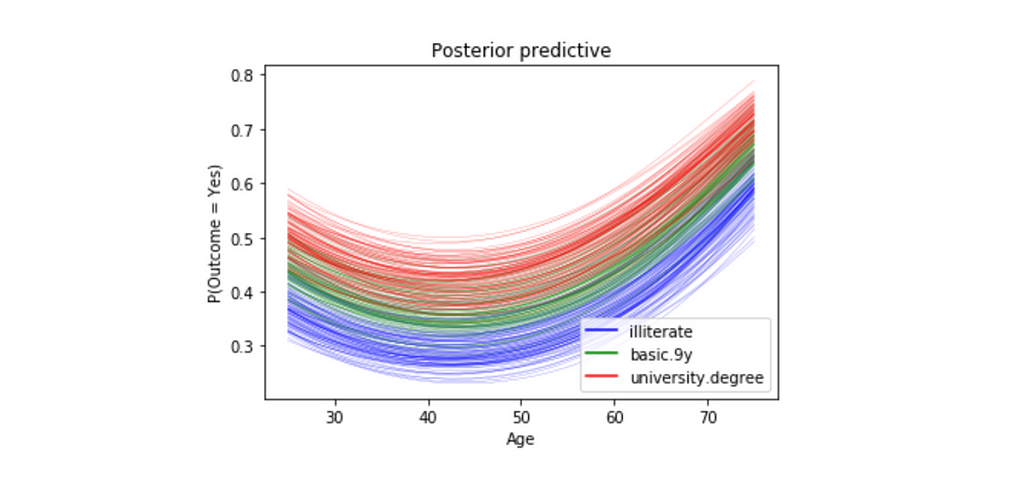
In this post, we will explore using Bayesian Logistic Regression in order to predict whether or not a customer will subscribe a term deposit after the marketing campaign the bank performed.

We want to be able to accomplish:

• How likely a customer to subscribe a term deposit?
• Experimenting of variables selection techniques.
• Explorations of the variables so serves as a good example of Exploratory Data Analysis and how that can guide the model creation and selection process.

I am sure you are familiar with the dataset. We built a logistic regression model using standard machine learning methods with this dataset a while ago. And today we are going to apply Bayesian methods to fit a logistic regression model and then interpret the resulting model parameters. Let’s get started!

The Data

The goal of this dataset is to create a binary classification model that predicts whether or not a customer will subscribe a term deposit after a marketing campaign the bank performed, based on many indicators. The target variable is given as y and takes on a value of 1 if the customer has subscribed and 0 otherwise.

This is an imbalanced class problem because there are significantly more customers did not subscribe the term deposit than the ones did.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pymc3 as pm
import arviz as az
import matplotlib.lines as mlines
import warnings
warnings.filterwarnings('ignore')
from collections import OrderedDict
import theano
import theano.tensor as tt
import itertools
from IPython.core.pylabtools import figsize
pd.set_option('display.max_columns', 30)
from sklearn.metrics import accuracy_score, f1_score, confusion_matrix

df = pd.read_csv('banking.csv')

As part of EDA, we will plot a few visualizations.

• Explore the target variable versus customers’ age using the stripplot function from seaborn:

sns.stripplot(x="y", y="age", data=df, jitter=True)
plt.show();

• Explore the target variable versus euribor3m using the stripplot function from seaborn:

sns.stripplot(x="y", y="euribor3m", data=df, jitter=True)
plt.show();

Nothing particularly interesting here.

The following is my way of making all of the variables numeric. You may have a better way of doing it.

Logistic Regression with One Independent Variable

We are going to begin with the simplest possible logistic model, using just one independent variable or feature, the duration.

outcome = df['y']
data = df[['age', 'job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'day_of_week', 'duration', 'campaign', 'pdays', 'previous', 'poutcome', 'euribor3m']]
data['outcome'] = outcome
data.corr()['outcome'].sort_values(ascending=False)

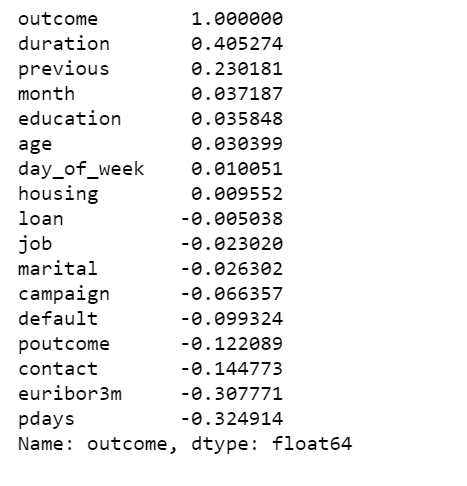
With the data in the right format, we can start building our first and simplest logistic model with PyMC3:

• Centering the data can help with the sampling.
• One of the deterministic variables θ is the output of the logistic function applied to the μ variable.
• Another deterministic variables bd is the boundary function.
• pm.math.sigmoid is the Theano function with the same name.

We are going to plot the fitted sigmoid curve and the decision boundary:

• The above plot shows non subscription vs. subscription (y = 0, y = 1).
• The S-shaped (green) line is the mean value of θ. This line can be interpreted as the probability of a subscription, given that we know that the last time contact duration(the value of the duration).
• The boundary decision is represented as a (black) vertical line. According to the boundary decision, the values of duration to the left correspond to y = 0 (non subscription), and the values to the right to y = 1 (subscription).

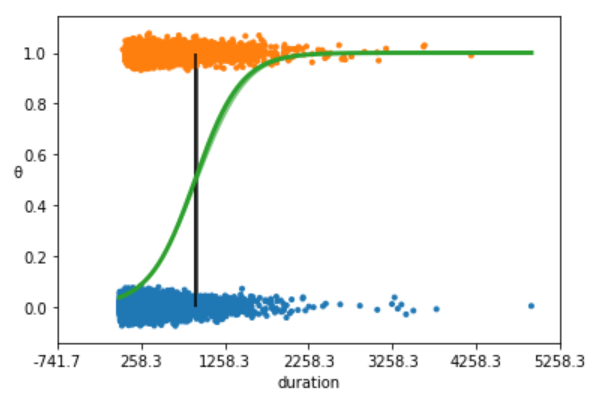
We summarize the inferred parameters values for easier analysis of the results and check how well the model did:

az.summary(trace_simple, var_names=['α', 'β'])

As you can see, the values of α and β are very narrowed defined. This is totally reasonable, given that we are fitting a binary fitted line to a perfectly aligned set of points.

Let’s run a posterior predictive check to explore how well our model captures the data. We can let PyMC3 do the hard work of sampling from the posterior for us:

ppc = pm.sample_ppc(trace_simple, model=model_simple, samples=500)
preds = np.rint(ppc['y_1'].mean(axis=0)).astype('int')

print('Accuracy of the simplest model:', accuracy_score(preds, data['outcome']))
print('f1 score of the simplest model:', f1_score(preds, data['outcome']))

Correlation of the Data

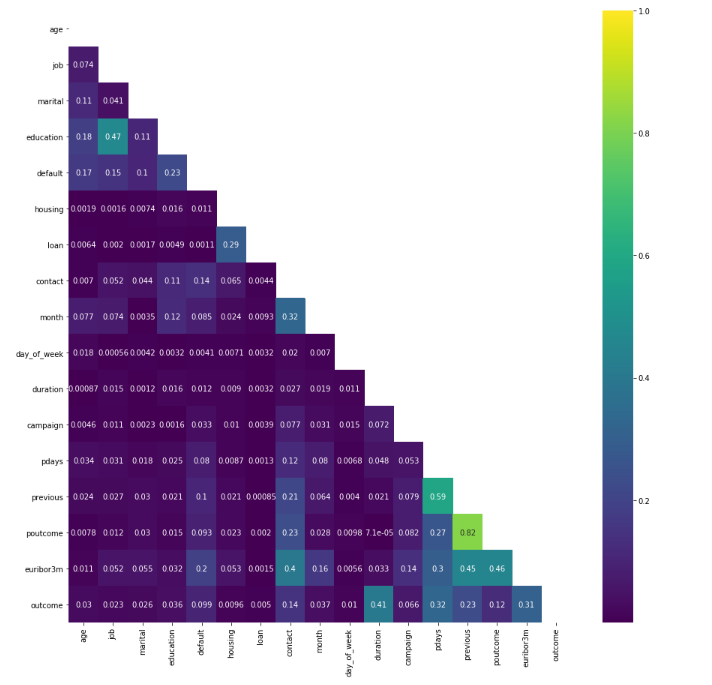
We plot a heat map to show the correlations between each variables.

plt.figure(figsize=(15, 15))
corr = data.corr() 
mask = np.tri(*corr.shape).T 
sns.heatmap(corr.abs(), mask=mask, annot=True, cmap='viridis');

• poutcome & previous have a high correlation, we can simply remove one of them, I decide to remove poutcome.
• There are not many strong correlations with the outcome variable. The highest positive correlation is 0.41.

Define logistic regression model using PyMC3 GLM method with multiple independent variables

• We assume that the probability of a subscription outcome is a function of age, job, marital, education, default, housing, loan, contact, month, day of week, duration, campaign, pdays, previous and euribor3m. We need to specify a prior and a likelihood in order to draw samples from the posterior.
• The interpretation formula is as follows:

logit = β0 + β1(age) + β2(age)2 + β3(job) + β4(marital) + β5(education) + β6(default) + β7(housing) + β8(loan) + β9(contact) + β10(month) + β11(day_of_week) + β12(duration) + β13(campaign) + β14(campaign) + β15(pdays) + β16(previous) + β17(poutcome) + β18(euribor3m) and y = 1 if outcome is yes and y = 0 otherwise.

• The log odds can then be converted to a probability of the output:

• For our problem, we are interested in finding the probability a customer will subscribe a term deposit given all the activities:

• With the math out of the way we can get back to the data. PyMC3 has a module glm for defining models using a patsy-style formula syntax. This seems really useful, especially for defining models in fewer lines of code.
• We use PyMC3 to draw samples from the posterior. The sampling algorithm used is NUTS, in which parameters are tuned automatically.
• We will use all these 18 variables and create the model using the formula defined above. The idea of adding a age2 is borrowed from this tutorial, and It would be interesting to compare models lately as well.
• We will also scale age by 10, it helps with model convergence.

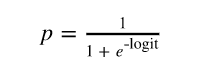
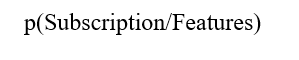
Above I only show part of the trace plot.

• This trace shows all of the samples drawn for all of the variables. On the left we can see the final approximate posterior distribution for the model parameters. On the right we get the individual sampled values at each step during the sampling.
• This glm defined model appears to behave in a very similar way, and finds the same parameter values as the conventionally-defined model we have created earlier.

I want to be able to answer questions like:

How do age and education affect the probability of subscribing a term deposit? Given a customer is married

• To answer this question, we will show how the probability of subscribing a term deposit changes with age for a few different education levels, and we want to study married customers.
• We will pass in three different linear models: one with education == 1 (illiterate), one with education == 5(basic.9y) and one with education == 8(university.degree).

• For all three education levels, the probability of subscribing a term deposit decreases with age until approximately at age 40, when the probability begins to increase.
• Every curve is blurry, this is because we are plotting 100 different curves for each level of education. Each curve is a draw from our posterior distribution.

Odds Ratio

• Does education of a person affects his or her subscribing to a term deposit? To do it we will use the concept of odds, and we can estimate the odds ratio of education like this:

b = trace['education']
plt.hist(np.exp(b), bins=20, normed=True)
plt.xlabel("Odds Ratio")
plt.show();

• We are 95% confident that the odds ratio of education lies within the following interval.

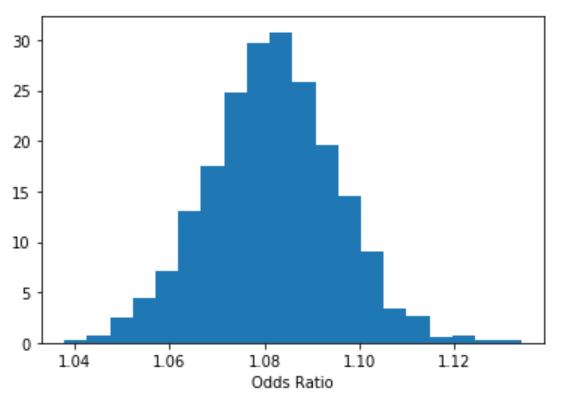
lb, ub = np.percentile(b, 2.5), np.percentile(b, 97.5)
print("P(%.3f < Odds Ratio < %.3f) = 0.95" % (np.exp(lb), np.exp(ub)))

• We can interpret something along those lines: “With probability 0.95 the odds ratio is greater than 1.055 and less than 1.108, so the education effect takes place because a person with a higher education level has at least 1.055 higher probability to subscribe to a term deposit than a person with a lower education level, while holding all the other independent variables constant.”
• We can estimate odds ratio and percentage effect for all the variables.

stat_df = pm.summary(trace)
stat_df['odds_ratio'] = np.exp(stat_df['mean'])
stat_df['percentage_effect'] = 100 * (stat_df['odds_ratio'] - 1)
stat_df

• We can interpret percentage_effect along those lines: “ With a one unit increase in education, the odds of subscribing to a term deposit increases by 8%. Similarly, for a one unit increase in euribor3m, the odds of subscribing to a term deposit decreases by 43%, while holding all the other independent variables constant.”

Credible Interval

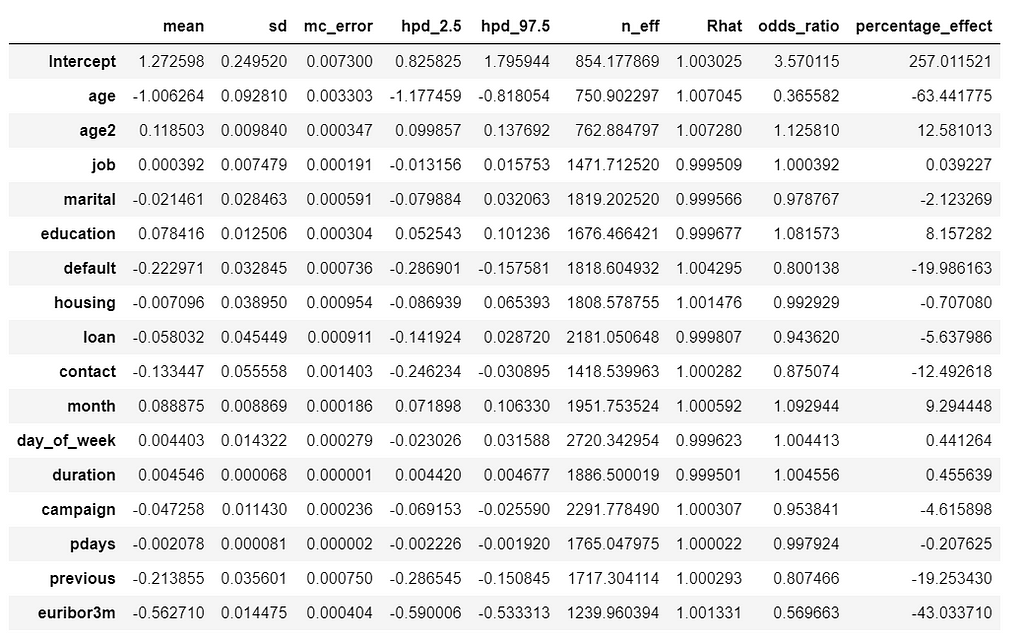
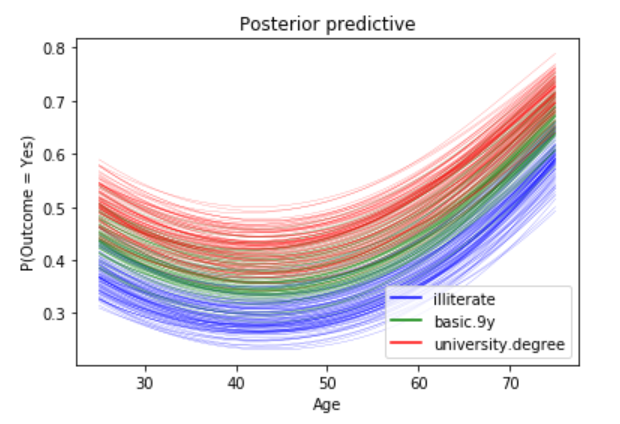
Its hard to show the entire forest plot, I only show part of it, but its enough for us to say that there’s a baseline probability of subscribing a term deposit. Beyond that, age has the biggest effect on subscribing, followed by contact.

Compare models using Widely-applicable Information Criterion (WAIC)

• If you remember, we added an age2 variable which is squared age. Now its the time to ask what effect it has on our model.
• WAIC is a measure of model fit that can be applied to Bayesian models and that works when the parameter estimation is done using numerical techniques. Read this paper to learn more.
• We’ll compare three models with increasing polynomial complexity. In our case, we are interested in the WAIC score.
• Now loop through all the models and calculate the WAIC.

• PyMC3 includes two convenience functions to help compare WAIC for different models. The first of this functions is compare which computes WAIC from a set of traces and models and returns a DataFrame which is ordered from lowest to highest WAIC.

model_trace_dict = dict()
for nm in ['k1', 'k2', 'k3']:
    models_lin[nm].name = nm
    model_trace_dict.update({models_lin[nm]: traces_lin[nm]})

dfwaic = pm.compare(model_trace_dict, ic='WAIC')
dfwaic

• We should prefer the model(s) with lower WAIC.
• The second convenience function takes the output of compare and produces a summary plot.

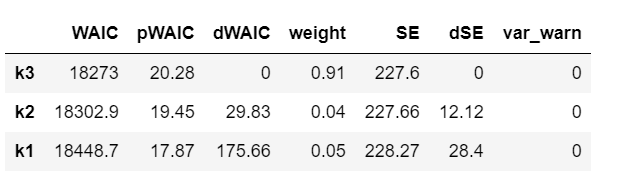
pm.compareplot(dfwaic);

• The empty circle represents the values of WAIC and the black error bars associated with them are the values of the standard deviation of WAIC.
• The value of the lowest WAIC is also indicated with a vertical dashed grey line to ease comparison with other WAIC values.
• The filled in black dots are the in-sample deviance of each model, which for WAIC is 2 pWAIC from the corresponding WAIC value.
• For all models except the top-ranked one, we also get a triangle, indicating the value of the difference of WAIC between that model and the top model, and a grey error bar indicating the standard error of the differences between the top-ranked WAIC and WAIC for each model.

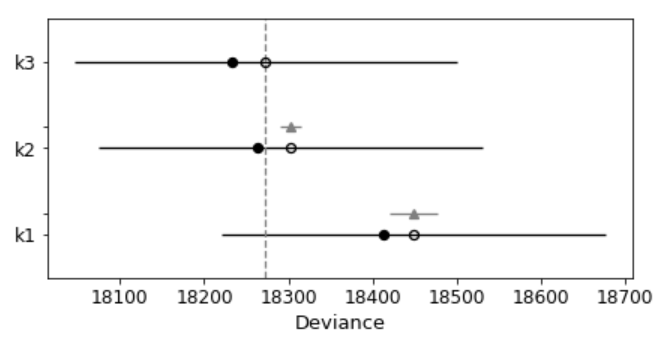
This confirms that the model that includes square of age is better than the model without.

Posterior predictive check

Unlike standard machine learning, Bayesian focused on model interpretability around a prediction. But I’am curious to know what we will get if we calculate the standard machine learning metrics.

We are going to calculate the metrics using the mean value of the parameters as a “most likely” estimate.

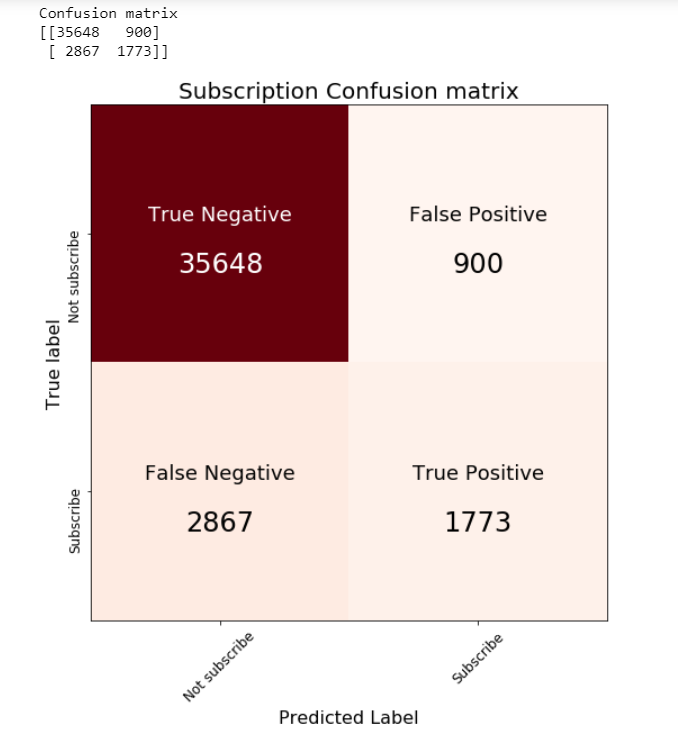
print('Accuracy of the full model: ', accuracy_score(preds, data['outcome']))
print('f1 score of the full model: ', f1_score(preds, data['outcome']))

Jupyter notebook can be found on Github. Have a great week!

References:

• GLM: Logistic Regression – PyMC3 3.6 documentation
• Model comparison – PyMC3 3.6 documentation

The book: Bayesian Analysis with Python, Second Edition

Building a Bayesian Logistic Regression with Python and PyMC3 was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Sounds like automatically categorize product description into its respective category (multi-class text classification problem). 300 classes sound too many, you may want to consolidate, or if the classes are imbalanced, you may want to take care of some more important classes first. Do you have other features, such as price or date time features, you may want to use them too.

Gaussian Inference, Posterior Predictive Checks, Group Comparison, Hierarchical Linear Regression

If you think Bayes’ theorem is counter-intuitive and Bayesian statistics, which builds upon Baye’s theorem, can be very hard to understand. I am with you.

There are countless reasons why we should learn Bayesian statistics, in particular, Bayesian statistics is emerging as a powerful framework to express and understand next-generation deep neural networks.

I believe that for the things we have to learn before we can do them, we learn by doing them. And nothing in life is so hard that we can’t make it easier by the way we take it.

So, this is my way of making it easier: Rather than too much of theories or terminologies at the beginning, let’s focus on the mechanics of Bayesian analysis, in particular, how to do Bayesian analysis and visualization with PyMC3 & ArviZ. Prior to memorizing the endless terminologies, we will code the solutions and visualize the results, and using the terminologies and theories to explain the models along the way.

PyMC3 is a Python library for probabilistic programming with a very simple and intuitive syntax. ArviZ, a Python library that works hand-in-hand with PyMC3 and can help us interpret and visualize posterior distributions.

And we will apply Bayesian methods to a practical problem, to show an end-to-end Bayesian analysis that move from framing the question to building models to eliciting prior probabilities to implementing in Python the final posterior distribution.

Before we start, let’s get some basic intuitions out of the way:

Bayesian models are also known as probabilistic models because they are built using probabilities. And Bayesian’s use probabilities as a tool to quantify uncertainty. Therefore, the answers we get are distributions not point estimates.

Bayesian Approach Steps

Step 1: Establish a belief about the data, including Prior and Likelihood functions.

Step 2, Use the data and probability, in accordance with our belief of the data, to update our model, check that our model agrees with the original data.

Step 3, Update our view of the data based on our model.

The Data

Since I am interested in using machine learning for price optimization, I decide to apply Bayesian methods to a Spanish High Speed Rail tickets pricing data set that can be found here. Appreciate The Gurus team for scraping the data set.

from scipy import stats
import arviz as az
import numpy as np
import matplotlib.pyplot as plt
import pymc3 as pm
import seaborn as sns
import pandas as pd
from theano import shared
from sklearn import preprocessing

print('Running on PyMC3 v{}'.format(pm.__version__))

data = pd.read_csv('renfe.csv')
data.drop('Unnamed: 0', axis = 1, inplace=True)
data = data.sample(frac=0.01, random_state=99)
data.head(3)

data.isnull().sum()/len(data)

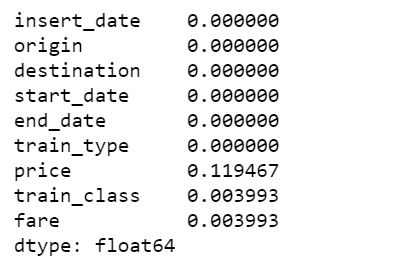
There are 12% of values in price column are missing, I decide to fill them with the mean of the respective fare types. Also fill the other two categorical columns with the most common values.

data['train_class'] = data['train_class'].fillna(data['train_class'].mode().iloc[0])
data['fare'] = data['fare'].fillna(data['fare'].mode().iloc[0])
data['price'] = data.groupby('fare').transform(lambda x: x.fillna(x.mean()))

Gaussian Inferences

az.plot_kde(data['price'].values, rug=True)
plt.yticks([0], alpha=0);

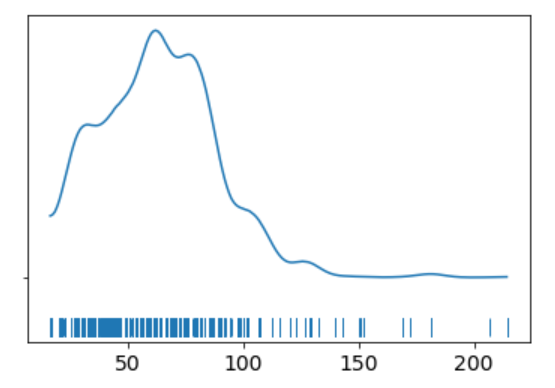
The KDE plot of the rail ticket price shows a Gaussian-like distribution, except for about several dozens of data points that are far away from the mean.

Let’s assume that a Gaussian distribution is a proper description of the rail ticket price. Since we do not know the mean or the standard deviation, we must set priors for both of them. Therefore, a reasonable model could be as follows.

Model

We will perform Gaussian inferences on the ticket price data. Here’s some of the modelling choices that go into this.

We would instantiate the Models in PyMC3 like this:

• Model specifications in PyMC3 are wrapped in a with-statement.

Choices of priors:

• μ, mean of a population. Normal distribution, very wide. I do not know the possible values of μ, I can set priors reflecting my ignorance. From experience I know that train ticket price can not be lower than 0 or higher than 300, so I set the boundaries of the uniform distribution to be 0 and 300. You may have different experience and set the different boundaries. That is totally fine. And if you have more reliable prior information than I do, please use it!
• σ, standard deviation of a population. Can only be positive, therefore use HalfNormal distribution. Again, very wide.

Choices for ticket price likelihood function:

• y is an observed variable representing the data that comes from a normal distribution with the parameters μ and σ.
• Draw 1000 posterior samples using NUTS sampling.

Using PyMC3, we can write the model as follows:

The y specifies the likelihood. This is the way in which we tell PyMC3 that we want to condition for the unknown on the knows (data).

We plot the gaussian model trace. This runs on a Theano graph under the hood.

az.plot_trace(trace_g);

• On the left, we have a KDE plot, — for each parameter value on the x-axis we get a probability on the y-axis that tells us how likely that parameter value is.
• On the right, we get the individual sampled values at each step during the sampling. From the trace plot, we can visually get the plausible values from the posterior.
• The above plot has one row for each parameter. For this model, the posterior is bi-dimensional, and so the above figure is showing the marginal distributions of each parameter.

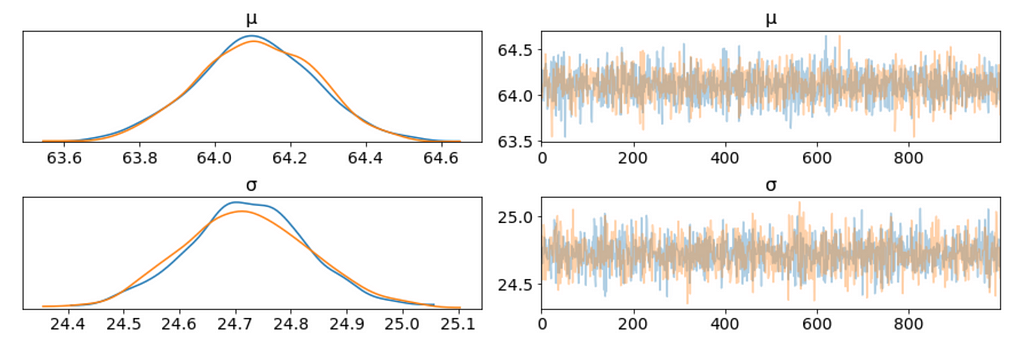
There are a couple of things to notice here:

• Our sampling chains for the individual parameters (left) seem well converged and stationary (there are no large drifts or other odd patterns).
• The maximum posterior estimate of each variable (the peak in the left side distributions) is very close to the true parameters.

We can plot a joint distributions of parameters.

az.plot_joint(trace_g, kind='kde', fill_last=False);

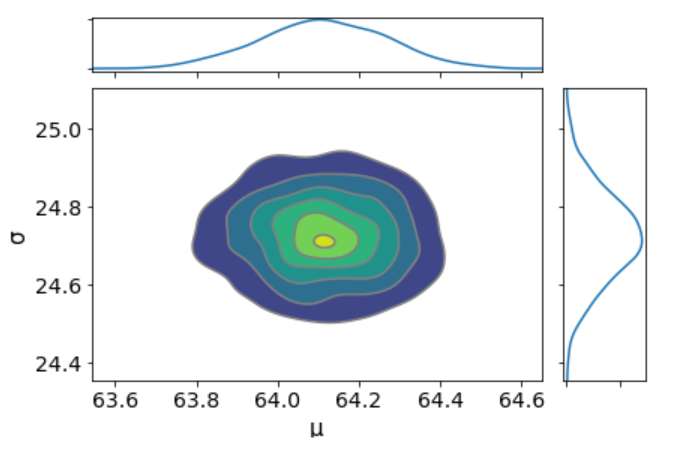
I don’t see any correlation between these two parameters. This means we probably do not have collinearity in the model. This is good.

We can also have a detailed summary of the posterior distribution for each parameter.

az.summary(trace_g)

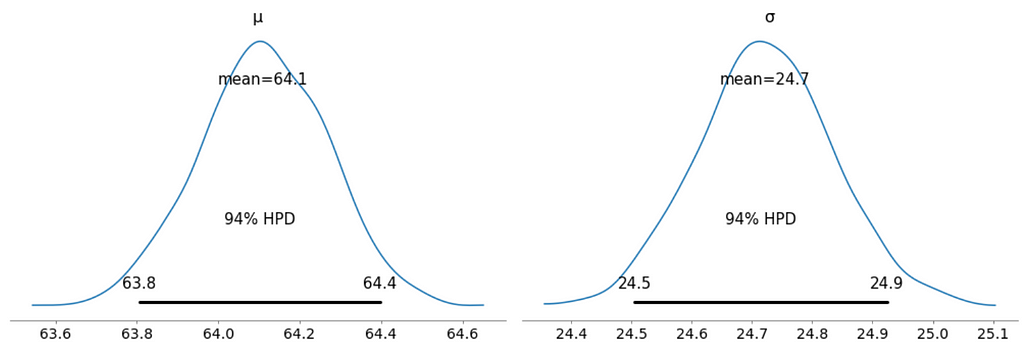
We can also see the above summary visually by generating a plot with the mean and Highest Posterior Density (HPD) of a distribution, and to interpret and report the results of a Bayesian inference.

az.plot_posterior(trace_g);

• Unlike Frequentist inference, in Bayesian inference, we get the entire distribution of the values.
• Every time ArviZ computes and reports a HPD, it will use, by default, a value of 94%.
• Please note that HPD intervals are not the same as confidence intervals.
• Here we can interpret as such that there is 94% probability the belief is between 63.8 euro and 64.4 euro for the mean ticket price.

We can verify the convergence of the chains formally using the Gelman Rubin test. Values close to 1.0 mean convergence.

pm.gelman_rubin(trace_g)

bfmi = pm.bfmi(trace_g)
max_gr = max(np.max(gr_stats) for gr_stats in pm.gelman_rubin(trace_g).values())
(pm.energyplot(trace_g, legend=False, figsize=(6, 4)).set_title("BFMI = {}nGelman-Rubin = {}".format(bfmi, max_gr)));

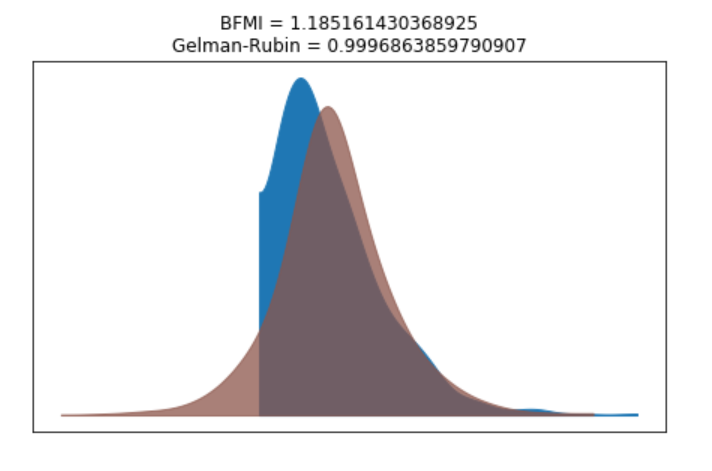
Our model has converged well and the Gelman-Rubin statistic looks fine.

Posterior Predictive Checks

• Posterior predictive checks (PPCs) are a great way to validate a model. The idea is to generate data from the model using parameters from draws from the posterior.
• Now that we have computed the posterior, we are going to illustrate how to use the simulation results to derive predictions.
• The following function will randomly draw 1000 samples of parameters from the trace. Then, for each sample, it will draw 25798 random numbers from a normal distribution specified by the values of μ and σ in that sample.

ppc = pm.sample_posterior_predictive(trace_g, samples=1000, model=model_g)

np.asarray(ppc['y']).shape

Now, ppc contains 1000 generated data sets (containing 25798 samples each), each using a different parameter setting from the posterior.

_, ax = plt.subplots(figsize=(10, 5))
ax.hist([y.mean() for y in ppc['y']], bins=19, alpha=0.5)
ax.axvline(data.price.mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');

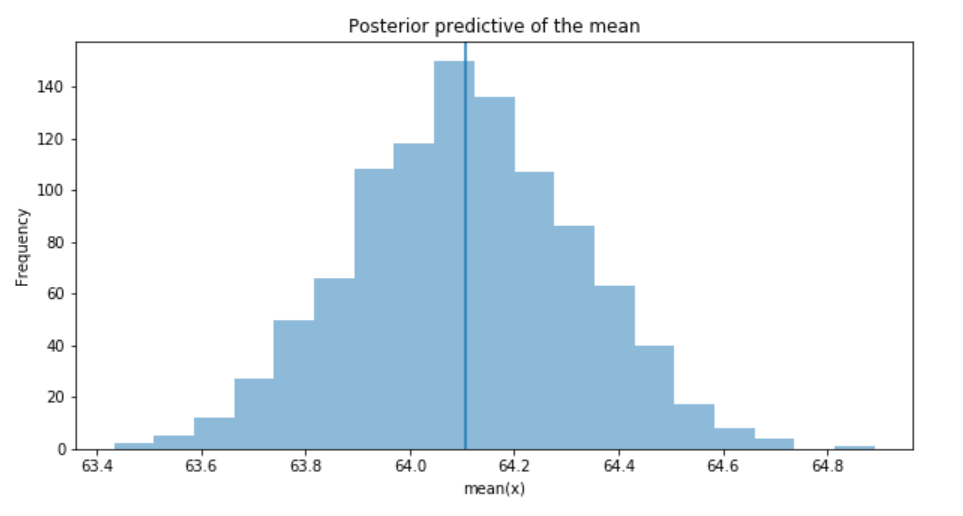
The inferred mean is very close to the actual rail ticket price mean.

Group Comparison

We may be interested in how price compare under different fare types. We are going to focus on estimating the effect size, that is, quantifying the difference between two fare categories. To compare fare categories, we are going to use the mean of each fare type. Because we are Bayesian, we will work to obtain a posterior distribution of the differences of means between fare categories.

We create three variables:

• The price variable, representing the ticket price.
• The idx variable, a categorical dummy variable to encode the fare categories with numbers.
• And finally the groups variable, with the number of fare categories (6)

price = data['price'].values
idx = pd.Categorical(data['fare'],
                     categories=['Flexible', 'Promo', 'Promo +', 'Adulto ida', 'Mesa', 'Individual-Flexible']).codes
groups = len(np.unique(idx))

The model for the group comparison problem is almost the same as the previous model. the only difference is that μ and σ are going to be vectors instead of scalar variables. This means that for the priors, we pass a shape argument and for the likelihood, we properly index the means and sd variables using the idx variable:

With 6 groups (fare categories), its a little hard to plot trace plot for μ and σ for every group. So, we create a summary table:

flat_fares = az.from_pymc3(trace=trace_groups)
fares_gaussian = az.summary(flat_fares)
fares_gaussian

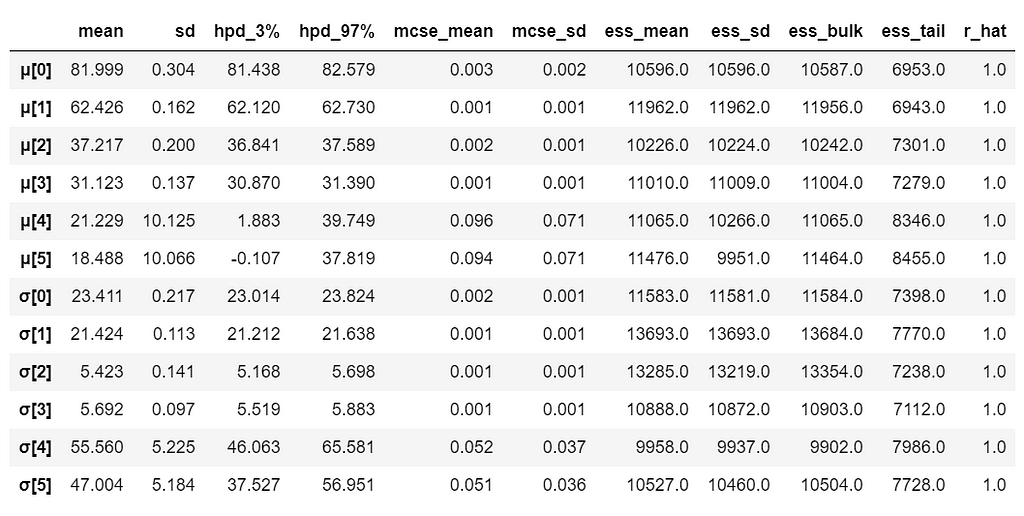
It is obvious that there are significant differences between groups (i.e. fare categories) on the mean.

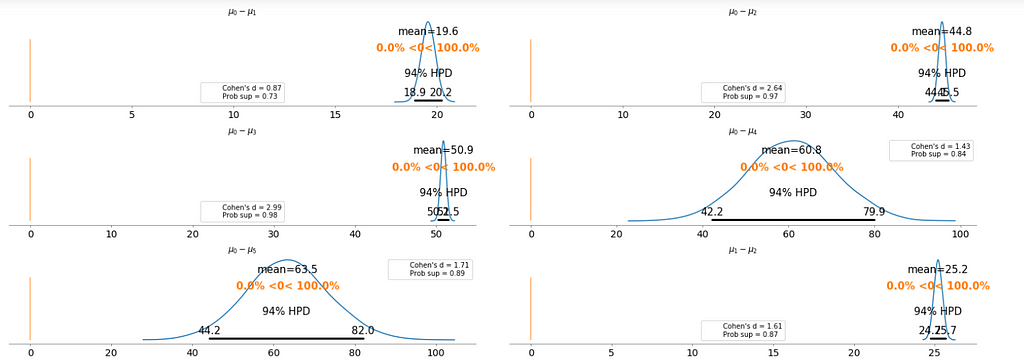
To make it clearer, we plot the difference between each fare category without repeating the comparison.

• Cohen’s d is an appropriate effect size for the comparison between two means. Cohen’s d introduces the variability of each group by using their standard deviations.
• probability of superiority (ps) is defined as the probability that a data point taken at random from one group has a larger value than one taken at random from another group.

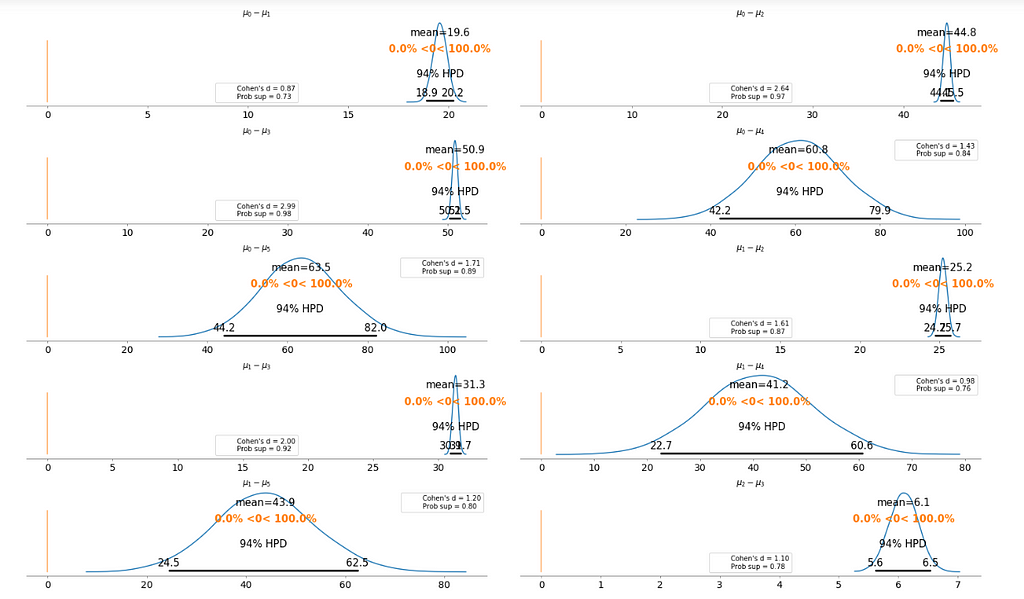
Basically, the above plot tells us that none of the above comparison cases where the 94% HPD includes the reference value of zero. This means for all the examples, we can rule out a difference of zero. The average differences range of 6.1 euro to 63.5 euro are large enough that it can justify for customers to purchase tickets according to different fare categories.

Bayesian Hierarchical Linear Regression

We want to build a model to estimate the rail ticket price of each train type, and, at the same time, estimate the price of all the train types. This type of model is known as a hierarchical model or multilevel model.

• Encoding the categorical variable.
• The idx variable, a categorical dummy variable to encode the train types with numbers.
• And finally the groups variable, with the number of train types (16)

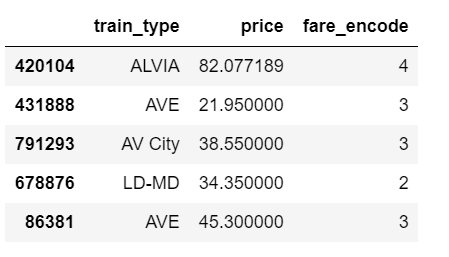
The relevant part of the data we will model looks as above. And we are interested in whether different train types affect the ticket price.

Hierarchical Model

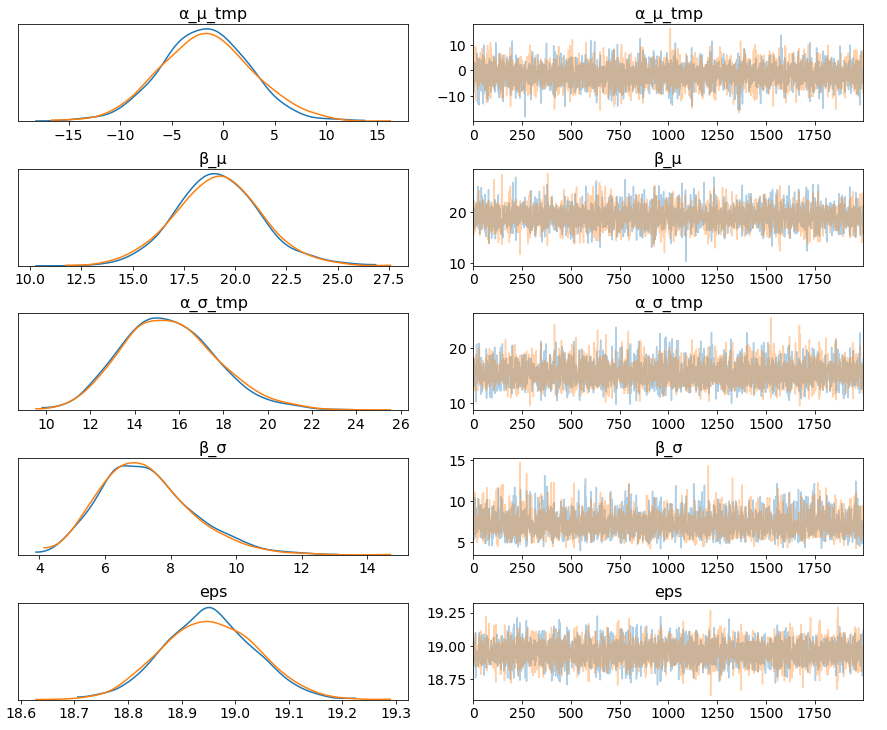
The marginal posteriors in the left column are highly informative, “α_μ_tmp” tells us the group mean price levels, “β_μ” tells us that purchasing fare category “Promo +” increases price significantly compare to fare type “Adulto ida”, and purchasing fare category “Promo” increases price significantly compare to fare type “Promo +”, and so on (no mass under zero).

pm.traceplot(hierarchical_trace, var_names=['α_tmp'], coords={'α_tmp_dim_0': range(5)});

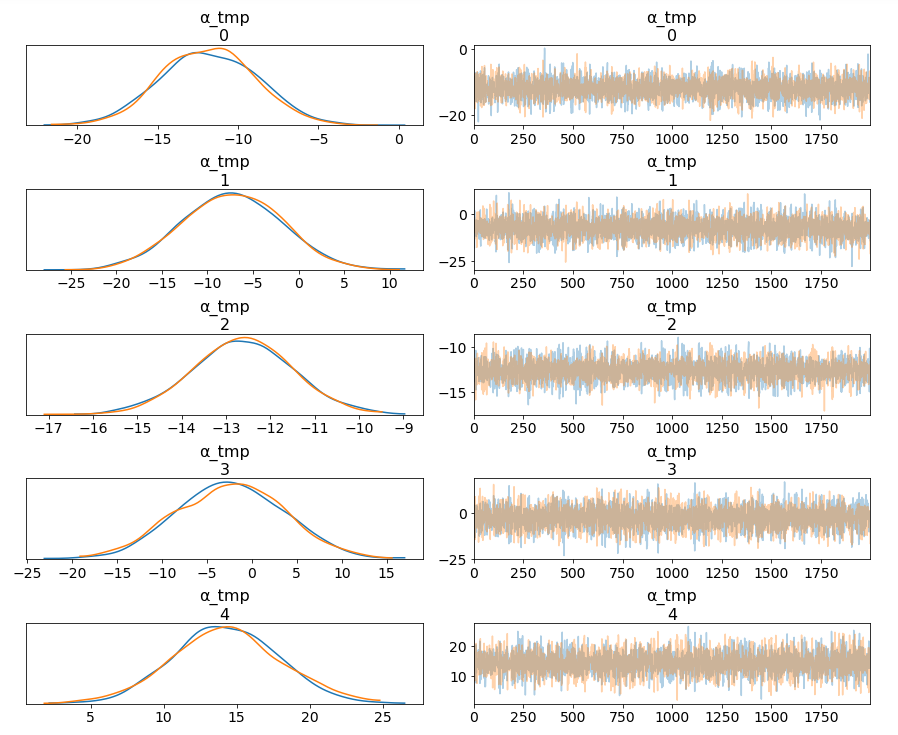
Among 16 train types, we may want to look at how 5 train types compare in terms of the ticket price. We can see by looking at the marginals for “α_tmp” that there is quite some difference in prices between train types; the different widths are related to how much confidence we have in each parameter estimate — the more measurements per train type, the higher our confidence will be.

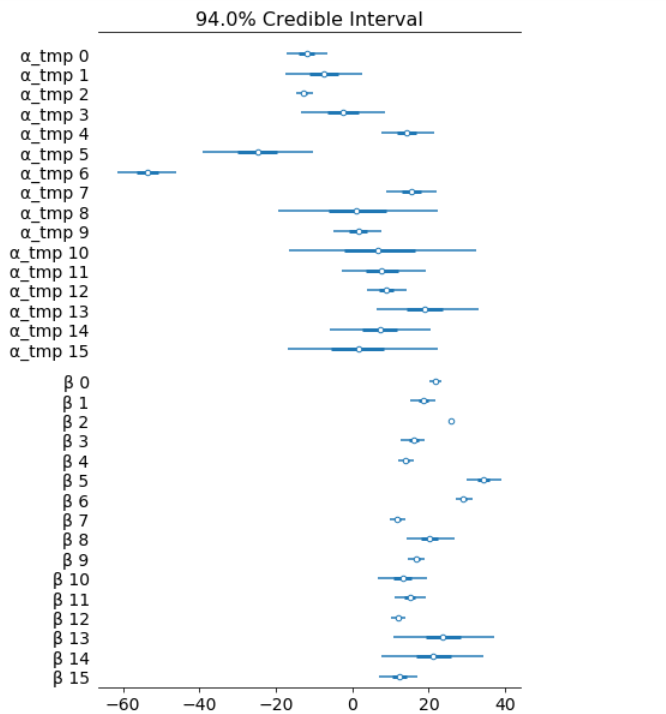
Having uncertainty quantification of some of our estimates is one of the powerful things about Bayesian modelling. We’ve got a Bayesian credible interval for the price of different train types.

az.plot_forest(hierarchical_trace, var_names=['α_tmp', 'β'], combined=True);

Lastly, we may want to compute r squared:

ppc = pm.sample_posterior_predictive(hierarchical_trace, samples=2000, model=hierarchical_model)
az.r2_score(data.price.values, ppc['fare_like'])

The objective of this post is to learn, practice and explain Bayesian, not to produce the best possible results from the data set. Otherwise, we would have gone with XGBoost directly.

Jupyter notebook can be found on Github, enjoy the rest of the week.

References:

• GLM: Hierarchical Linear Regression – PyMC3 3.6 documentation
• A Hierarchical model for Rugby prediction – PyMC3 3.6 documentation

The book: Bayesian Analysis with Python

Hands On Bayesian Statistics with Python, PyMC3 & ArviZ was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Interpretation for Text Classification

Last week, I gave a talk on “Hands-on Feature Engineering for NLP” at QCon New York. As a very small part of the presentation, I gave a brief demo on how LIME & SHAP work in terms of text classification explainability.

I decided to write a blog post about them because they are fun, easy to use and visually compelling.

All machine learning models that operate in higher dimensions than what can be directly visualized by the human mind can be referred as black box models which come down to the interpretability of the models. In particular in the field of NLP, it’s always the case that the dimension of the features are very huge, explaining feature importance is getting much more complicated.

LIME & SHAP help us provide an explanation not only to end users but also ourselves about how a NLP model works.

Using the Stack Overflow questions tags classification data set, we are going to build a multi-class text classification model, then applying LIME & SHAP separately to explain the model. Because we have done text classification many times before, we will quickly build the NLP models and focus on the models interpretability.

Data Pre-processing, Feature Engineering and Logistic Regression

Our objective here is not to produce the highest results. I wanted to dive into LIME & SHAP as soon as possible and that’s what happened next.

Interpreting text predictions with LIME

From now on, it’s the fun part. The following code snippets were largely borrowed from LIME tutorial.

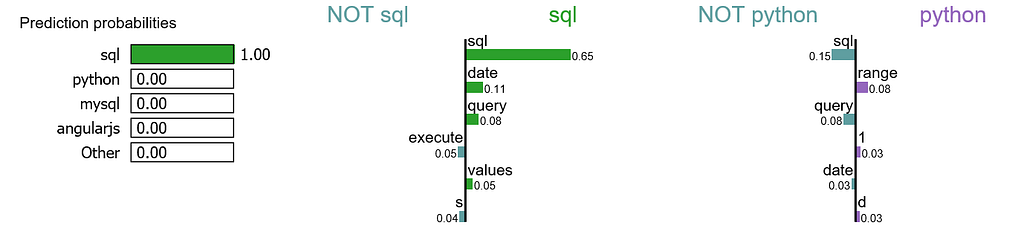
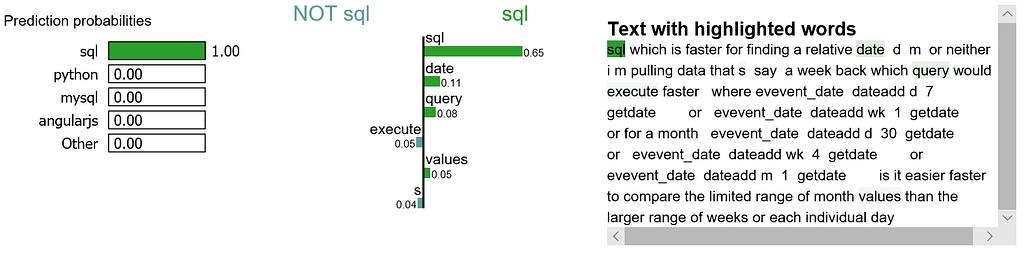
We randomly select a document in test set, it happens to be a document that labeled as sql, and our model predicts it as sql as well. Using this document, we generate explanations for label 4 which is sql and label 8 which is python.

print ('Explanation for class %s' % class_names[4])
print ('n'.join(map(str, exp.as_list(label=4))))

print ('Explanation for class %s' % class_names[8])
print ('n'.join(map(str, exp.as_list(label=8))))

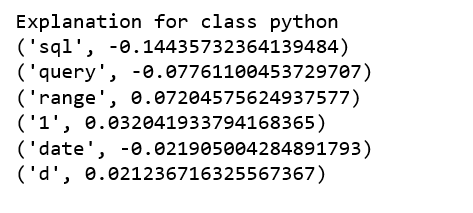
It is obvious that this document has the highest explanation for label sql. We also notice that the positive and negative signs are with respect to a particular label, such as word “sql” is positive towards class sql while negative towards class python, and vice versa.

We are going to generate labels for the top 2 classes for this document.

exp = explainer.explain_instance(X_test[idx], c.predict_proba, num_features=6, top_labels=2)
print(exp.available_labels())

It gives us sql and python.

exp.show_in_notebook(text=False)

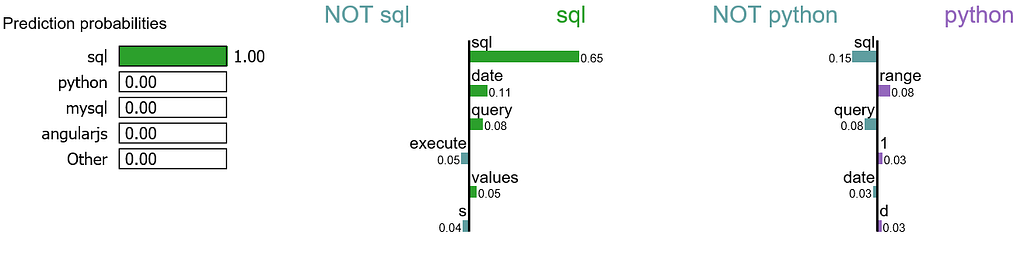
Let me try to explain this visualization:

• For this document, word “sql” has the highest positive score for class sql.
• Our model predicts this document should be labeled as sql with the probability of 100%.
• If we remove word “sql” from the document, we would expect the model to predict label sql with the probability at 100% — 65% = 35%.
• On the other hand, word “sql” is negative for class python, and our model has learned that word “range” has a small positive score for class python.

We may want to zoom in and study the explanations for class sql, as well as the document itself.

exp.show_in_notebook(text=y_test[idx], labels=(4,))

Interpreting text predictions with SHAP

The following process were learned from this tutorial.

• After model is trained, we use the first 200 training documents as our background data set to integrate over, and to create a SHAP explainer object.
• We get the attribution values for individual predictions on a subset of the test set.
• Transform the index to words.
• Use SHAP’s summary_plot method to show the top features impacting model predictions.

attrib_data = X_train[:200]
explainer = shap.DeepExplainer(model, attrib_data)
num_explanations = 20
shap_vals = explainer.shap_values(X_test[:num_explanations])

words = processor._tokenizer.word_index
word_lookup = list()
for i in words.keys():
  word_lookup.append(i)

word_lookup = [''] + word_lookup
shap.summary_plot(shap_vals, feature_names=word_lookup, class_names=tag_encoder.classes_)

• Word “want” is the biggest signal word used by our model, contribute most to class jquery predictions.
• Word “php” is the 4th biggest signal word used by our model, contributing most to class php of course.
• On the other hand, word “php” is likely to have a negative signal to the other class because it is unlikely to see word “php” to appear in a python document.

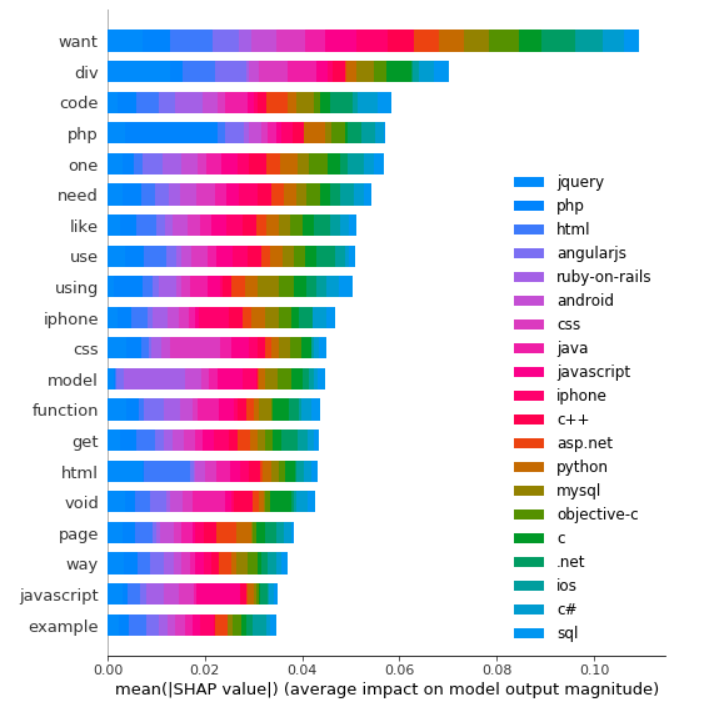
There are a lot to learn in terms of machine learning interpretability with LIME & SHAP. I have only covered a tiny piece for NLP. Jupyter notebook can be found on Github. Enjoy the fun!

Explain NLP models with LIME & SHAP was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Unsupervised Anomaly Detection for Univariate & Multivariate Data.

Anomaly detection is the process of identifying unexpected items or events in data sets, which differ from the norm. And anomaly detection is often applied on unlabeled data which is known as unsupervised anomaly detection. Anomaly detection has two basic assumptions:

• Anomalies only occur very rarely in the data.
• Their features differ from the normal instances significantly.

Univariate Anomaly Detection

Before we get to Multivariate anomaly detection, I think its necessary to work through a simple example of Univariate anomaly detection method in which we detect outliers from a distribution of values in a single feature space.

We are using the Super Store Sales data set that can be downloaded from here, and we are going to find patterns in Sales and Profit separately that do not conform to expected behavior. That is, spotting outliers for one variable at a time.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib
from sklearn.ensemble import IsolationForest

Distribution of the Sales

df = pd.read_excel("Superstore.xls")
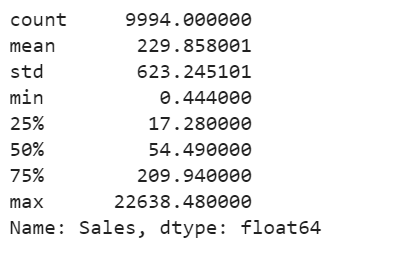
df['Sales'].describe()

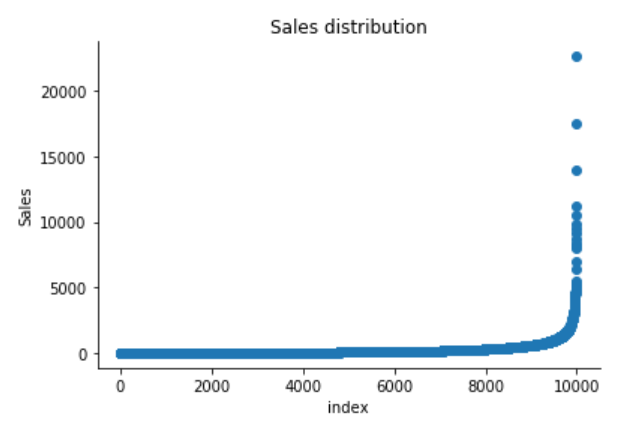
plt.scatter(range(df.shape[0]), np.sort(df['Sales'].values))
plt.xlabel('index')
plt.ylabel('Sales')
plt.title("Sales distribution")
sns.despine()

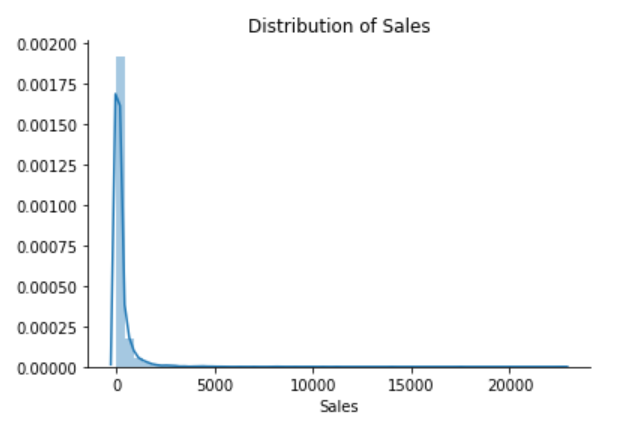
sns.distplot(df['Sales'])
plt.title("Distribution of Sales")
sns.despine()

print("Skewness: %f" % df['Sales'].skew())
print("Kurtosis: %f" % df['Sales'].kurt())

The Superstore’s sales distribution is far from a normal distribution, and it has a positive long thin tail, the mass of the distribution is concentrated on the left of the figure. And the tail sales distribution far exceeds the tails of the normal distribution.

There are one region where the data has low probability to appear which is on the right side of the distribution.

Distribution of the Profit

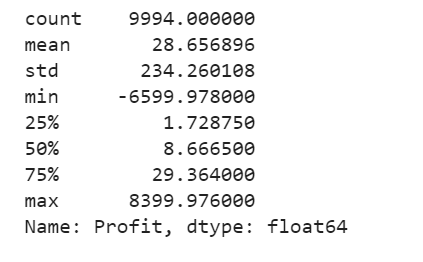
df['Profit'].describe()

plt.scatter(range(df.shape[0]), np.sort(df['Profit'].values))
plt.xlabel('index')
plt.ylabel('Profit')
plt.title("Profit distribution")
sns.despine()

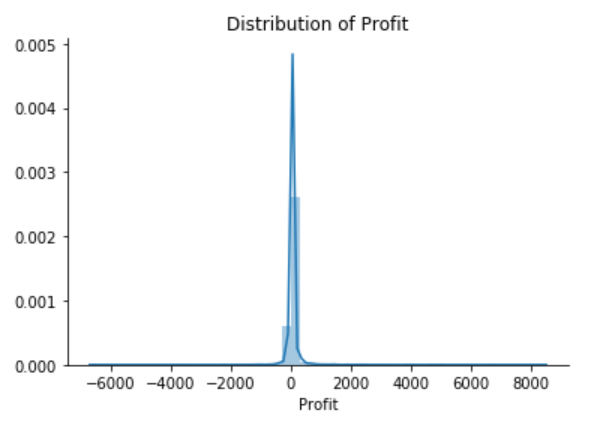
sns.distplot(df['Profit'])
plt.title("Distribution of Profit")
sns.despine()

print("Skewness: %f" % df['Profit'].skew())
print("Kurtosis: %f" % df['Profit'].kurt())

The Superstore’s Profit distribution has both a positive tail and negative tail. However, the positive tail is longer than the negative tail. So the distribution is positive skewed, and the data are heavy-tailed or profusion of outliers.

There are two regions where the data has low probability to appear: one on the right side of the distribution, another one on the left.

Univariate Anomaly Detection on Sales

Isolation Forest is an algorithm to detect outliers that returns the anomaly score of each sample using the IsolationForest algorithm which is based on the fact that anomalies are data points that are few and different. Isolation Forest is a tree-based model. In these trees, partitions are created by first randomly selecting a feature and then selecting a random split value between the minimum and maximum value of the selected feature.

The following process shows how IsolationForest behaves in the case of the Susperstore’s sales, and the algorithm was implemented in Sklearn and the code was largely borrowed from this tutorial

• Trained IsolationForest using the Sales data.
• Store the Sales in the NumPy array for using in our models later.
• Computed the anomaly score for each observation. The anomaly score of an input sample is computed as the mean anomaly score of the trees in the forest.
• Classified each observation as an outlier or non-outlier.
• The visualization highlights the regions where the outliers fall.

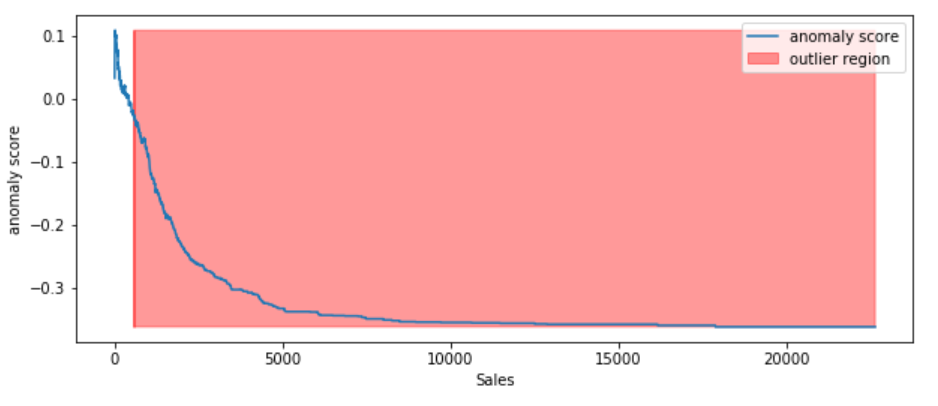
According to the above results and visualization, It seems that Sales that exceeds 1000 would be definitely considered as an outlier.

Visually investigate one anomaly

df.iloc[10]

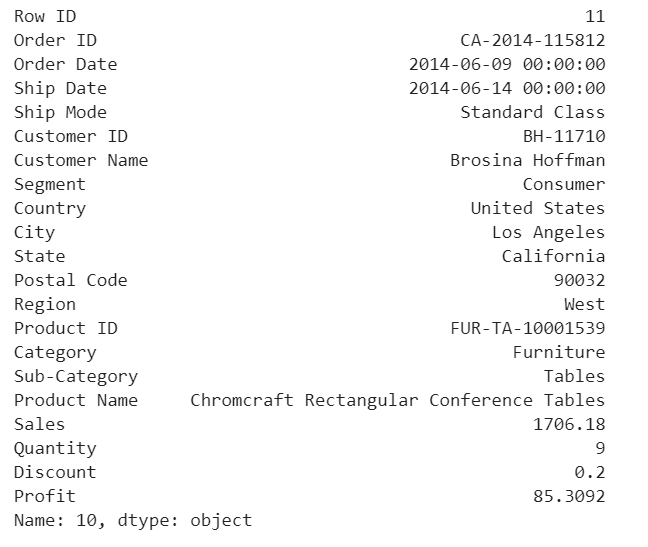
This purchase seems normal to me expect it was a larger amount of sales compared with the other orders in the data.

Univariate Anomaly Detection on Profit

• Trained IsolationForest using the Profit variable.
• Store the Profit in the NumPy array for using in our models later.
• Computed the anomaly score for each observation. The anomaly score of an input sample is computed as the mean anomaly score of the trees in the forest.
• Classified each observation as an outlier or non-outlier.
• The visualization highlights the regions where the outliers fall.

Visually investigate some of the anomalies

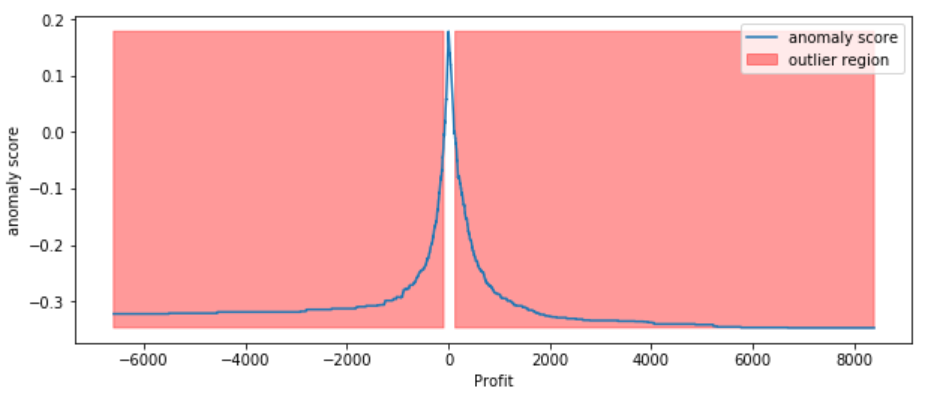
According to the above results and visualization, It seems that Profit that below -100 or exceeds 100 would be considered as an outlier, let’s visually examine one example each that determined by our model and to see whether they make sense.

df.iloc[3]

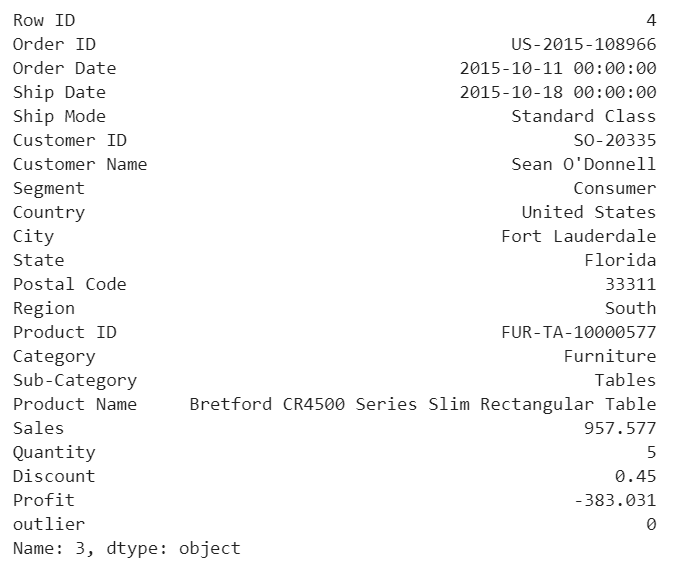
Any negative profit would be an anomaly and should be further investigate, this goes without saying

df.iloc[1]

Our model determined that this order with a large profit is an anomaly. However, when we investigate this order, it could be just a product that has a relatively high margin.

The above two visualizations show the anomaly scores and highlighted the regions where the outliers are. As expected, the anomaly score reflects the shape of the underlying distribution and the outlier regions correspond to low probability areas.

However, Univariate analysis can only get us thus far. We may realize that some of these anomalies that determined by our models are not the anomalies we expected. When our data is multidimensional as opposed to univariate, the approaches to anomaly detection become more computationally intensive and more mathematically complex.

Multivariate Anomaly Detection

Most of the analysis that we end up doing are multivariate due to complexity of the world we are living in. In multivariate anomaly detection, outlier is a combined unusual score on at least two variables.

So, using the Sales and Profit variables, we are going to build an unsupervised multivariate anomaly detection method based on several models.

We are using PyOD which is a Python library for detecting anomalies in multivariate data. The library was developed by Yue Zhao.

Sales & Profit

When we are in business, we expect that Sales & Profit are positive correlated. If some of the Sales data points and Profit data points are not positive correlated, they would be considered as outliers and need to be further investigated.

sns.regplot(x="Sales", y="Profit", data=df)
sns.despine();

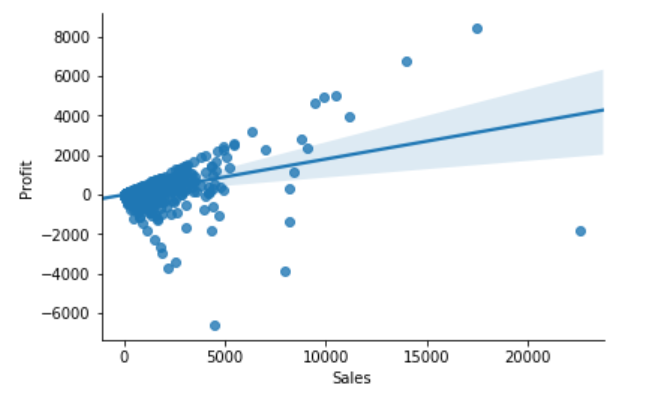
From the above correlation chart, we can see that some of the data points are obvious outliers such as extreme low and extreme high values.

Cluster-based Local Outlier Factor (CBLOF)

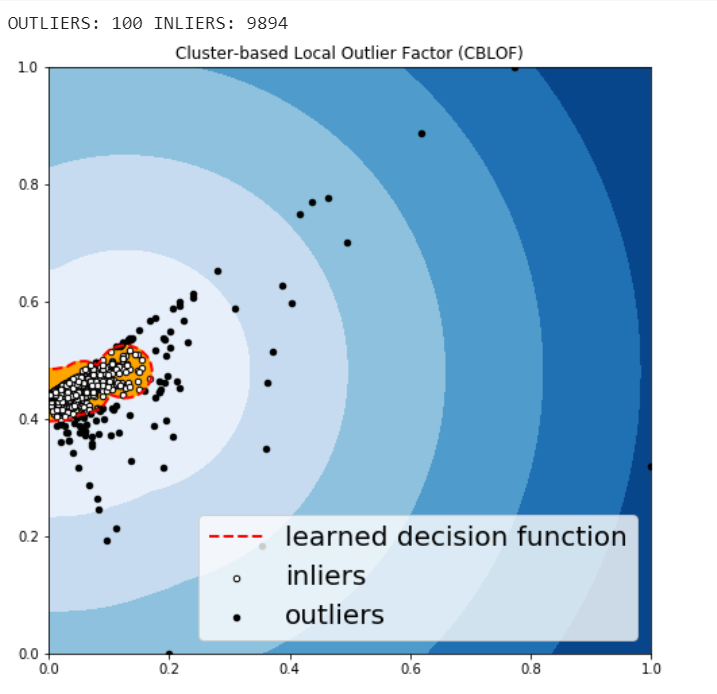
The CBLOF calculates the outlier score based on cluster-based local outlier factor. An anomaly score is computed by the distance of each instance to its cluster center multiplied by the instances belonging to its cluster. PyOD library includes the CBLOF implementation.

The following code are borrowed from PyOD tutorial combined with this article.

• Scaling Sales and Profit to between zero and one.
• Arbitrarily set outliers fraction as 1% based on trial and best guess.
• Fit the data to the CBLOF model and predict the results.
• Use threshold value to consider a data point is inlier or outlier.
• Use decision function to calculate the anomaly score for every point.

Histogram-based Outlier Detection (HBOS)

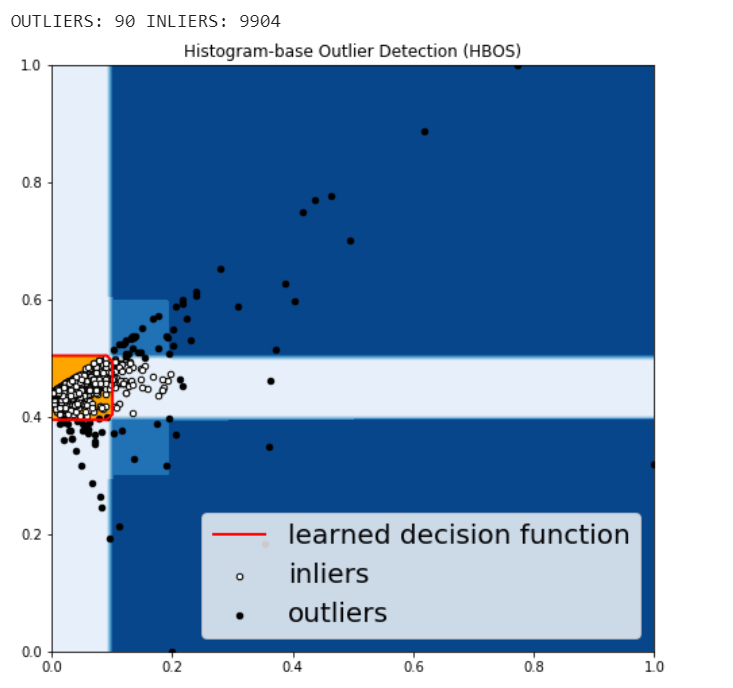
HBOS assumes the feature independence and calculates the degree of anomalies by building histograms. In multivariate anomaly detection, a histogram for each single feature can be computed, scored individually and combined at the end. When using PyOD library, the code are very similar with the CBLOF.

Isolation Forest

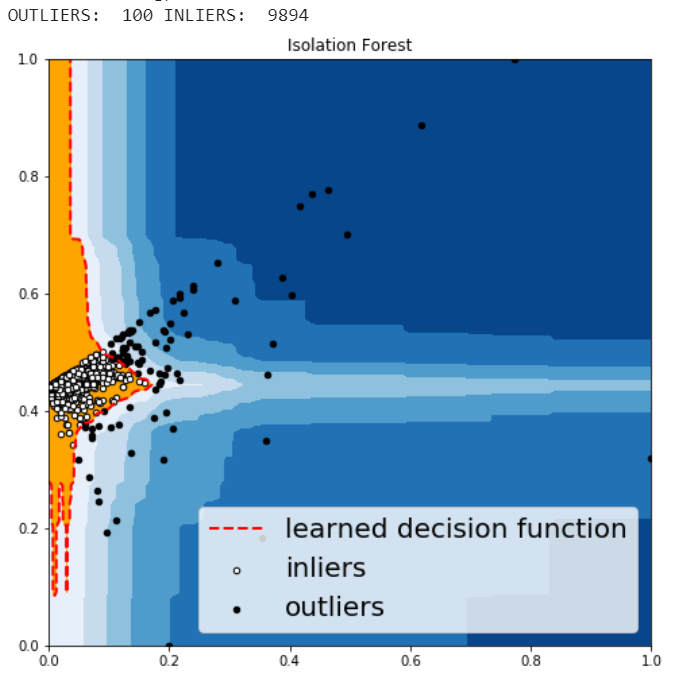
Isolation Forest is similar in principle to Random Forest and is built on the basis of decision trees. Isolation Forest isolates observations by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of that selected feature.

The PyOD Isolation Forest module is a wrapper of Scikit-learn Isolation Forest with more functionalities.

K – Nearest Neighbors (KNN)

KNN is one of the simplest methods in anomaly detection. For a data point, its distance to its kth nearest neighbor could be viewed as the outlier score.

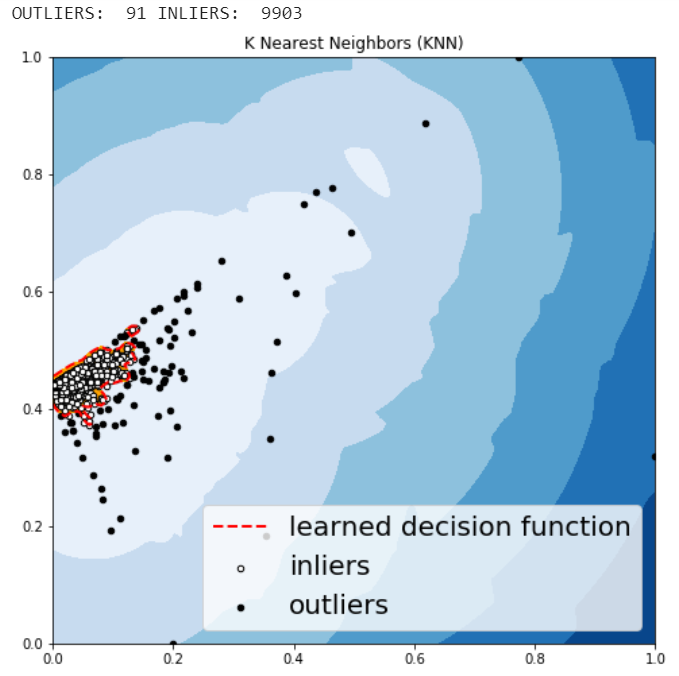
The anomalies predicted by the above four algorithms were not very different.

Visually investigate some of the anomalies

We may want to investigate each of the outliers that determined by our model, for example, let’s look in details for a couple of outliers that determined by KNN, and try to understand what make them anomalies.

df.iloc[1995]

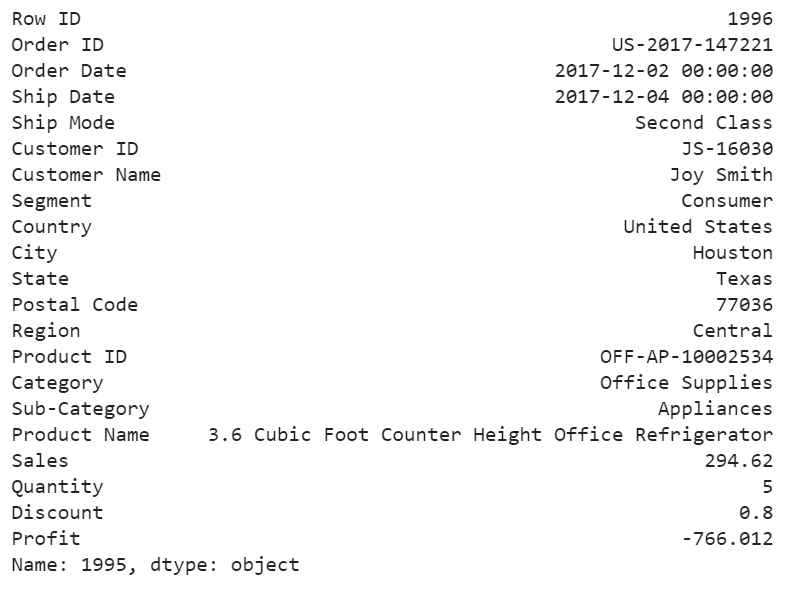
For this particular order, a customer purchased 5 products with total price at 294.62 and profit at lower than -766, with 80% discount. It seems like a clearance. We should be aware of the loss for each product we sell.

df.iloc[9649]

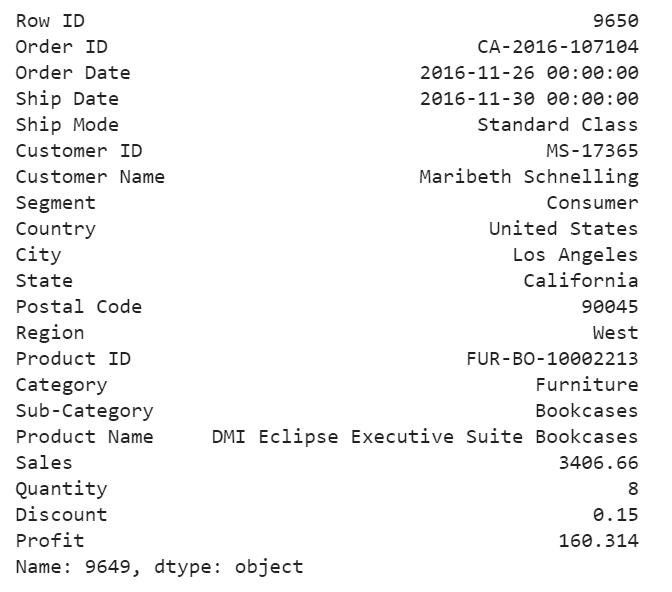
For this purchase, it seems to me that the profit at around 4.7% is too small and the model determined that this order is an anomaly.

df.iloc[9270]

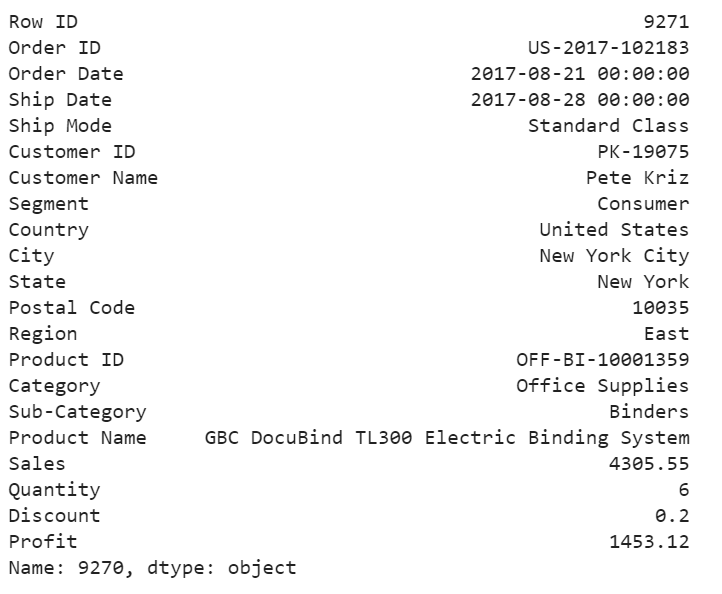
For the above order, a customer purchased 6 product at 4305 in total price, after 20% discount, we still get over 33% of the profit. We would love to have more of these kind of anomalies.

Jupyter notebook for the above analysis can be found on Github. Enjoy the rest of the week.

Anomaly Detection for Dummies was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.