Bayesian Modeling Airlines Customer Service Twitter Response Time

Student’s t-distribution, Poisson distribution, Negative Binomial distribution, Hierarchical modeling and Regression
Twitter conducted a study recently in the US, found that customers were willing to pay nearly $20 more to travel with an airline that had responded to their tweet in under six minutes. When they got a response over 67 minutes after their tweet, they would only pay $2 more to fly with that airline.
When I came across Customer Support on Twitter dataset, I couldn’t help but wanted to model and compare airlines customer service twitter response time.
I wanted to be able to answer questions like:
- Are there significant differences on customer service twitter response time among all the airlines in the data?
- Is the weekend affect response time?
- Do longer tweets take longer time to respond?
- Which airline has the shortest customer service twitter response time and vice versa?
The data
It is a large dataset contains hundreds of companies from all kinds of industries. The following data wrangling process will accomplish:
- Get customer inquiry, and corresponding response from the company in every row.
- Convert datetime columns to datetime data type.
- Calculate response time to minutes.
- Select only airline companies in the data.
- Any customer inquiry that takes longer than 60 minutes will be filtered out. We are working on requests that get response in 60 minutes.
- Create time attributes and response word count.
https://medium.com/media/9d8cc66aa77dae417cd2246b510ddf2b/href
Response time distribution
plt.figure(figsize=(10,5))
sns.distplot(df['response_time'], kde=False)
plt.title('Frequency of response by response time')
plt.xlabel('Response time (minutes)')
plt.ylabel('Number of responses');
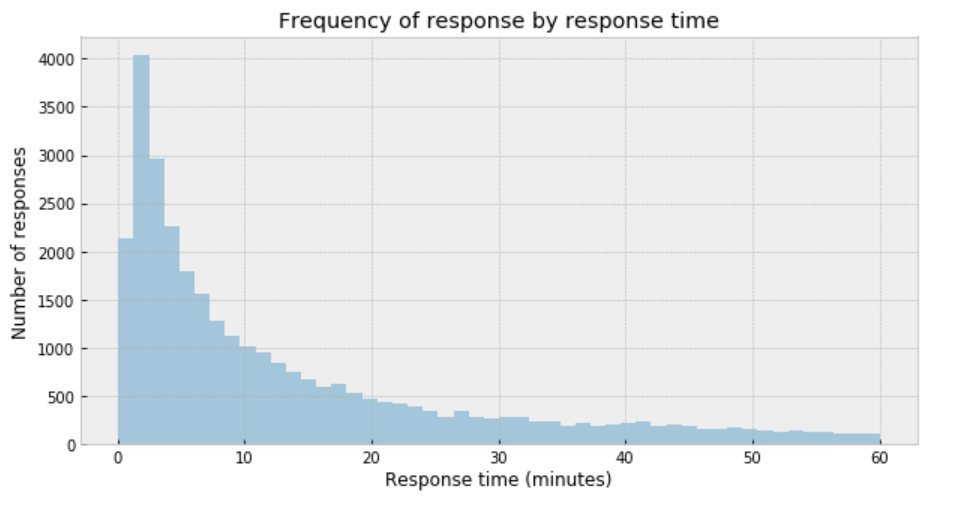
My immediate impression is that a Gaussian distribution is not a proper description of the data.
Student’s t-distribution
One useful option when dealing with outliers and Gaussian distributions is to replace the Gaussian likelihood with a Student’s t-distribution. This distribution has three parameters: the mean (𝜇), the scale (𝜎) (analogous to the standard deviation), and the degrees of freedom (𝜈).
- Set the boundaries of the uniform distribution of the mean to be 0 and 60.
- 𝜎 can only be positive, therefore use HalfNormal distribution.
- set 𝜈 as an exponential distribution with a mean of 1.
https://medium.com/media/c927243a9e1b9abe286dc505c48653d1/href
MCMC diagnostics
- From the following trace plot, we can visually get the plausible values of 𝜇 from the posterior.
- We should compare this result with those from the the result we obtained analytically.
az.plot_trace(trace_t[:1000], var_names = ['μ']);

df.response_time.mean()
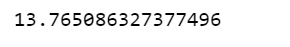
- The left plot shows the distribution of values collected for 𝜇. What we get is a measure of uncertainty and credible values of 𝜇 between 7.4 and 7.8 minutes.
- It is obvious that samples that have been drawn from distributions that are significantly different from the target distribution.
Posterior predictive check
One way to visualize is to look if the model can reproduce the patterns observed in the real data. For example, how close are the inferred means to the actual sample mean:
ppc = pm.sample_posterior_predictive(trace_t, samples=1000, model=model_t)
_, ax = plt.subplots(figsize=(10, 5))
ax.hist([n.mean() for n in ppc['y']], bins=19, alpha=0.5)
ax.axvline(df['response_time'].mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');
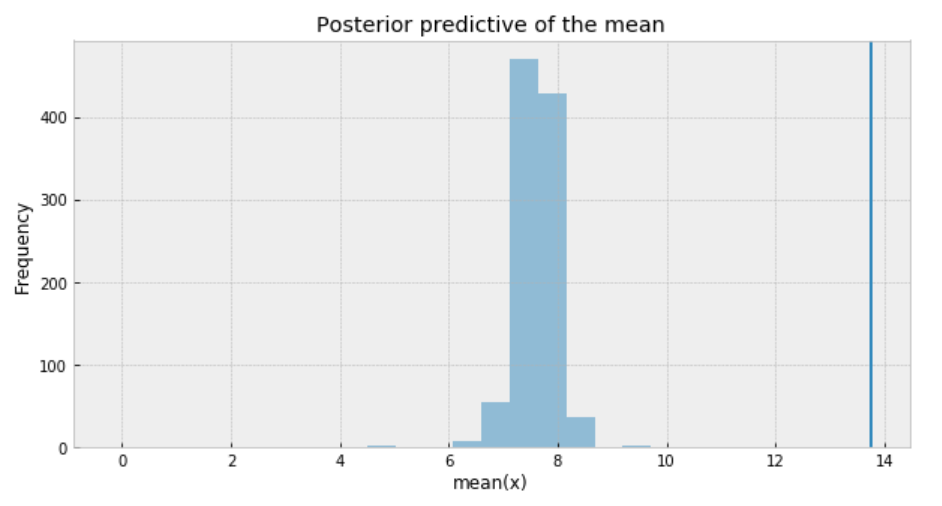
The inferred mean is so far away from the actual sample mean. This confirms that Student’s t-distribution is not a proper choice for our data.
Poisson distribution
Poisson distribution is generally used to describe the probability of a given number of events occurring on a fixed time/space interval. Thus, the Poisson distribution assumes that the events occur independently of each other and at a fixed interval of time and/or space. This discrete distribution is parametrized using only one value 𝜇, which corresponds to the mean and also the variance of the distribution.
https://medium.com/media/88200a01173117a5fe4003d8ceeb2f0b/href
MCMC diagnostics
az.plot_trace(trace_p);

The measure of uncertainty and credible values of 𝜇 is between 13.22 and 13.34 minutes. It sounds way better already.
Autocorrelations
We want the autocorrelation drops with increasing x-axis in the plot. Because this indicates a low degree of correlation between our samples.
_ = pm.autocorrplot(trace_p, var_names=['μ'])
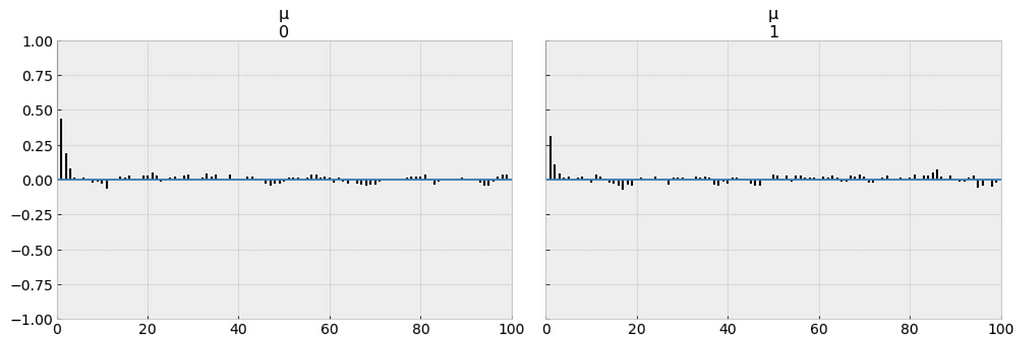
Our samples from the Poisson model has dropped to low values of autocorrelation, which is a good sign.
Posterior predictive check
We use posterior predictive check to “look for systematic discrepancies between real and simulated data”. There are multiple ways to do posterior predictive check, and I’d like to check if my model makes sense in various ways.
y_ppc_p = pm.sample_posterior_predictive(
trace_p, 100, model_p, random_seed=123)
y_pred_p = az.from_pymc3(trace=trace_p, posterior_predictive=y_ppc_p)
az.plot_ppc(y_pred_p, figsize=(10, 5), mean=False)
plt.xlim(0, 60);
Interpretation:
- The single (black) line is a kernel density estimate (KDE) of the data and the many purple lines are KDEs computed from each one of the 100 posterior predictive samples. The purple lines reflect the uncertainty we have about the inferred distribution of the predicted data.
- From the above plot, I can’t consider the scale of a Poisson distribution as a reasonable practical proxy for the standard deviation of the data even after removing outliers.
Posterior predictive check
ppc = pm.sample_posterior_predictive(trace_p, samples=1000, model=model_p)
_, ax = plt.subplots(figsize=(10, 5))
ax.hist([n.mean() for n in ppc['y']], bins=19, alpha=0.5)
ax.axvline(df['response_time'].mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');
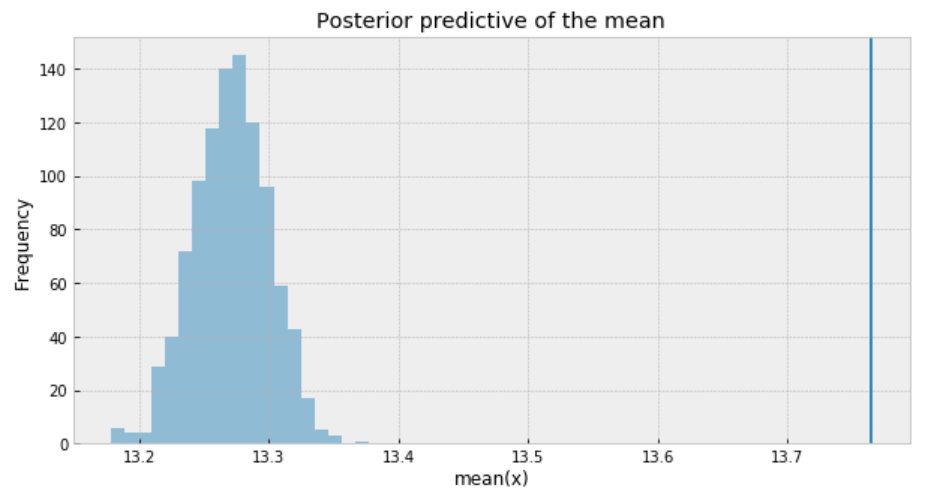
- The inferred means to the actual sample mean are much closer than what we got from Student’s t-distribution. But still, there is a small gap.
- The problem with using a Poisson distribution is that mean and variance are described by the same parameter. So one way to solve this problem is to model the data as a mixture of Poisson distribution with rates coming from a gamma distribution, which gives us the rationale to use the negative-binomial distribution.
Negative binomial distribution
Negative binomial distribution has very similar characteristics to the Poisson distribution except that it has two parameters (𝜇 and 𝛼) which enables it to vary its variance independently of its mean.
https://medium.com/media/5979510cd27f69dc726e5eeba9574b01/href
MCMC diagnostics
az.plot_trace(trace_n, var_names=['μ', 'α']);
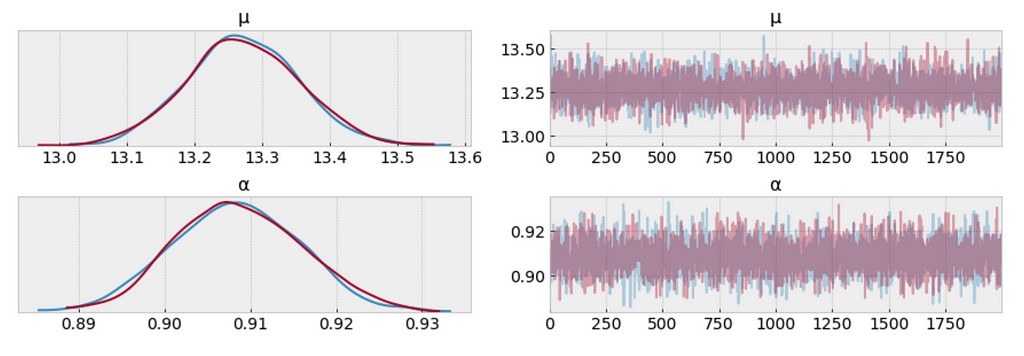
The measure of uncertainty and credible values of 𝜇 is between 13.0 and 13.6 minutes, and it is very closer to the target sample mean.
Posterior predictive check
y_ppc_n = pm.sample_posterior_predictive(
trace_n, 100, model_n, random_seed=123)
y_pred_n = az.from_pymc3(trace=trace_n, posterior_predictive=y_ppc_n)
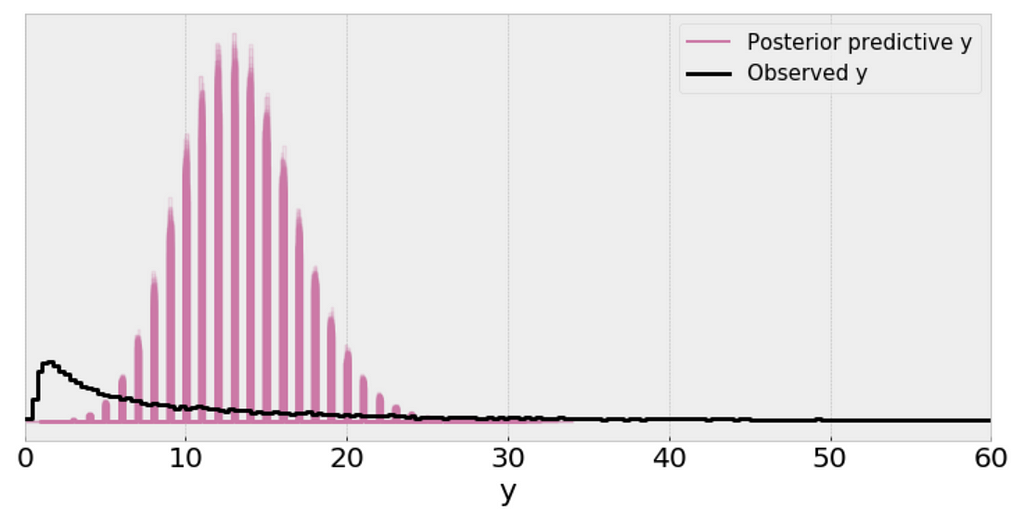
az.plot_ppc(y_pred_n, figsize=(10, 5), mean=False)
plt.xlim(0, 60);
Using the Negative binomial distribution in our model leads to predictive samples that seem to better fit the data in terms of the location of the peak of the distribution and also its spread.
Posterior predictive check
ppc = pm.sample_posterior_predictive(trace_n, samples=1000, model=model_n)
_, ax = plt.subplots(figsize=(10, 5))
ax.hist([n.mean() for n in ppc['y_est']], bins=19, alpha=0.5)
ax.axvline(df['response_time'].mean())
ax.set(title='Posterior predictive of the mean', xlabel='mean(x)', ylabel='Frequency');
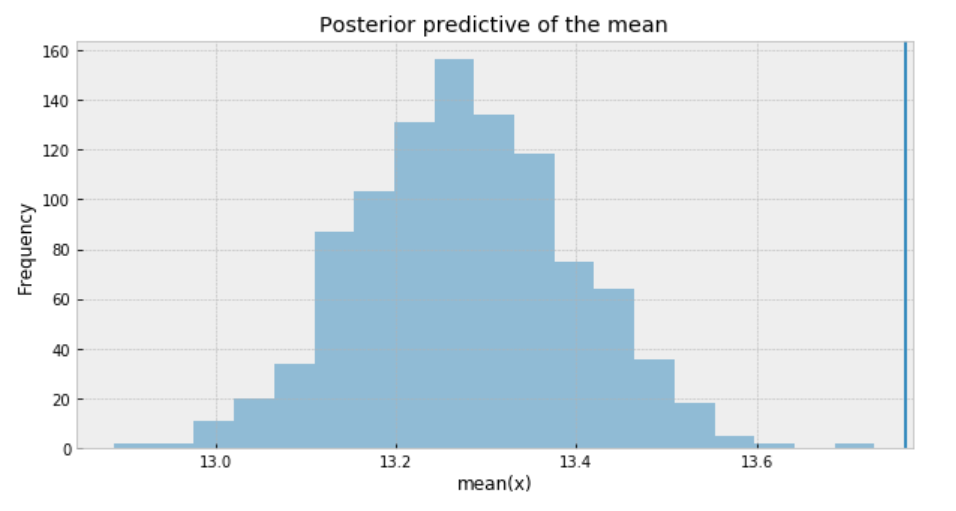
To sum it up, the following are what we get for the measure of uncertainty and credible values of (𝜇):
- Student t-distribution: 7.4 to 7.8 minutes
- Poisson distribution: 13.22 to 13.34 minutes
- Negative Binomial distribution: 13.0 to 13.6 minutes.
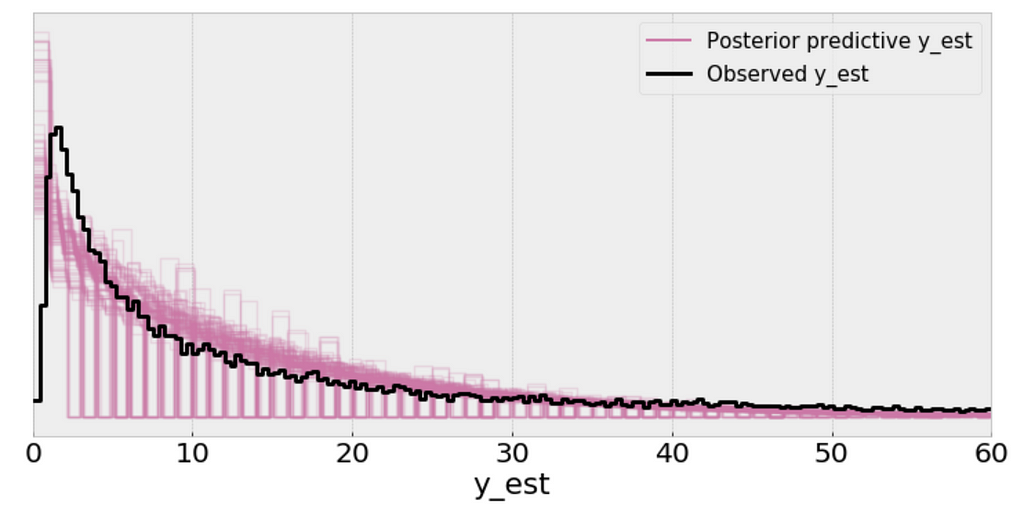
Posterior predictive distribution
https://medium.com/media/30e11e4826d9d4b8cc3d54e91077daec/href
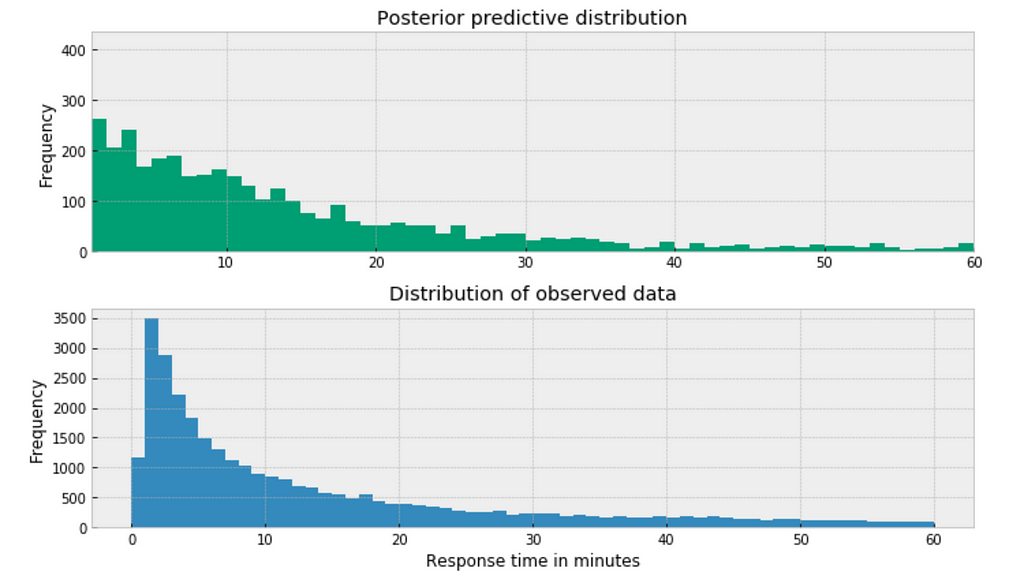
The posterior predictive distribution somewhat resembles the distribution of the observed data, suggesting that the Negative binomial model is a more appropriate fit for the underlying data.
Bayesian methods for hierarchical modeling
- We want to study each airline as a separated entity. We want to build a model to estimate the response time of each airline and, at the same time, estimate the response time of the entire data. This type of model is known as a hierarchical model or multilevel model.
- My intuition would suggest that different airline has different response time. The customer service twitter response from AlaskaAir might be faster than the response from AirAsia for example. As such, I decide to model each airline independently, estimating parameters μ and α for each airline.
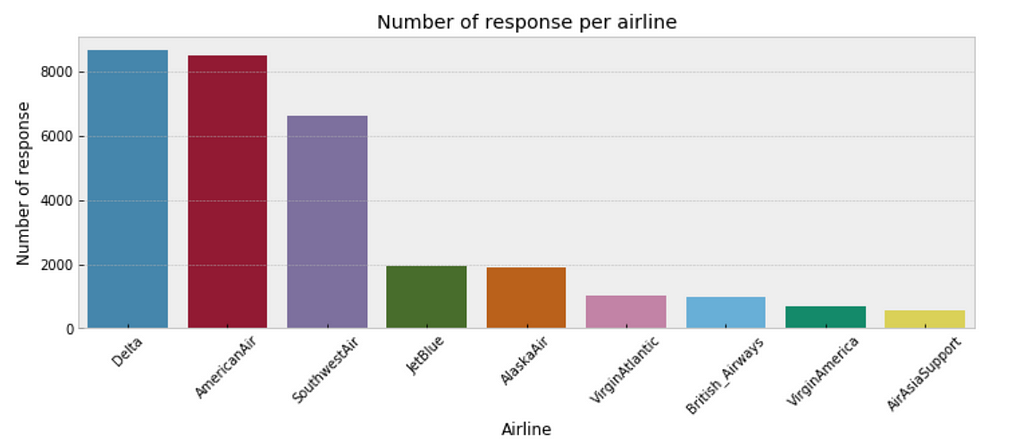
- One consideration is that some airlines may have fewer customer inquiries from twitter than others. As such, our estimates of response time for airlines with few customer inquires will have a higher degree of uncertainty than airlines with a large number of customer inquiries. The below plot illustrates the discrepancy in sample size per airline.
plt.figure(figsize=(12,4))
sns.countplot(x="author_id_y", data=df, order = df['author_id_y'].value_counts().index)
plt.xlabel('Airline')
plt.ylabel('Number of response')
plt.title('Number of response per airline')
plt.xticks(rotation=45);
Bayesian modeling each airline with negative binomial distribution
https://medium.com/media/4cdc4a72b3aede34b23dbb275d318aa4/href
Posterior predictive distribution for each airline
https://medium.com/media/139d5455997414082cd04ff48a930649/href
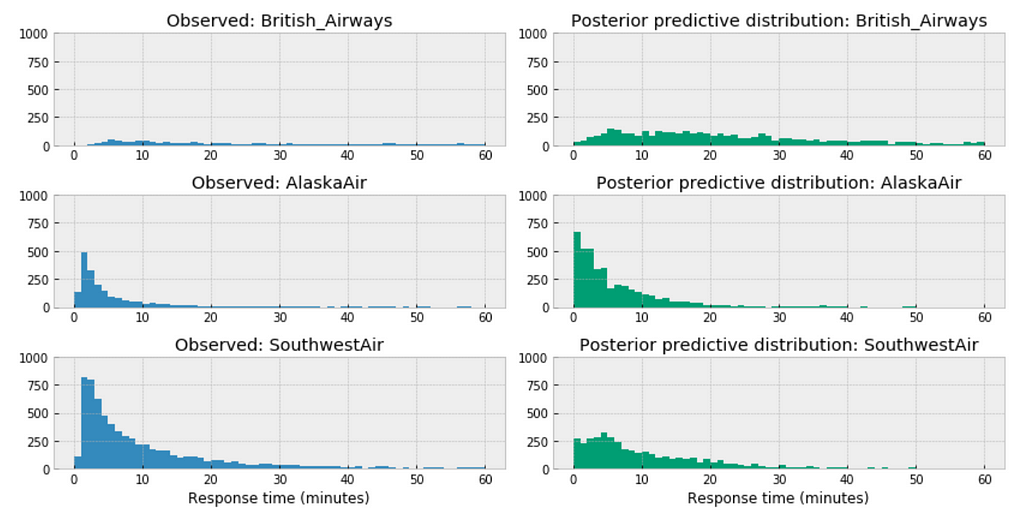
Observations:
- Among the above three airlines, British Airways’ posterior predictive distribution vary considerably to AlaskaAir and SouthwestAir. The distribution of British Airways towards right.
- This could accurately reflect the characteristics of its customer service twitter response time, means in general it takes longer for British Airways to respond than those of AlaskaAir or SouthwestAir.
- Or it could be incomplete due to small sample size, as we have way more data from Southwest than from British airways.
https://medium.com/media/a44e953f4ed2177f1b19ba489bcb0bc7/href
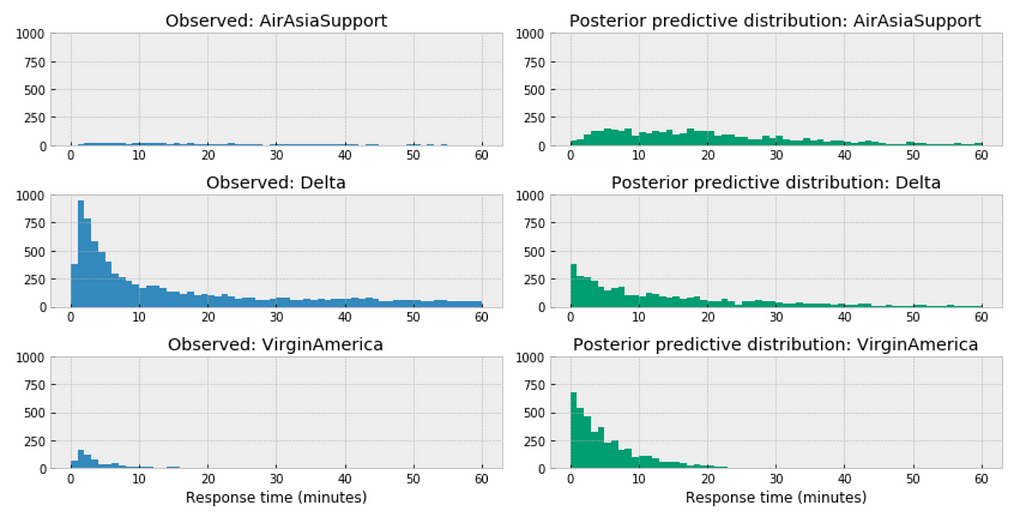
Similar here, among the above three airlines, the distribution of AirAsia towards right, this could accurately reflect the characteristics of its customer service twitter response time, means in general, it takes longer for AirAsia to respond than those of Delta or VirginAmerica. Or it could be incomplete due to small sample size.
https://medium.com/media/0c0a9ee55f4bd298907e0d10f79f1f71/href
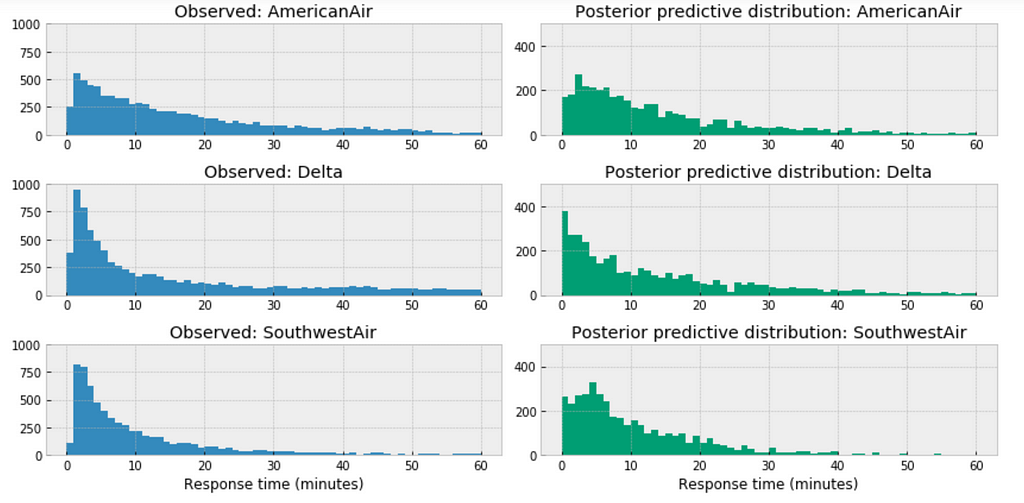
For the airlines we have relative sufficient data, for example, when we compare the above three large airlines in the United States, the posterior predictive distribution do not seem to vary significantly.
Bayesian Hierarchical Regression
The variables for the model:
df = df[['response_time', 'author_id_y', 'created_at_y_is_weekend', 'word_count']]
formula = 'response_time ~ ' + ' + '.join(['%s' % variable for variable in df.columns[1:]])
formula

In the following code snippet, we:
- Convert categorical variables to integer.
- Estimate a baseline parameter value 𝛽0 for each airline customer service response time.
- Estimate all the other parameter across the entire population of the airlines in the data.
https://medium.com/media/3076b071ea036ac663f5e91609ca1cb3/href
MCMC diagnostics
az.plot_trace(trace_hr);
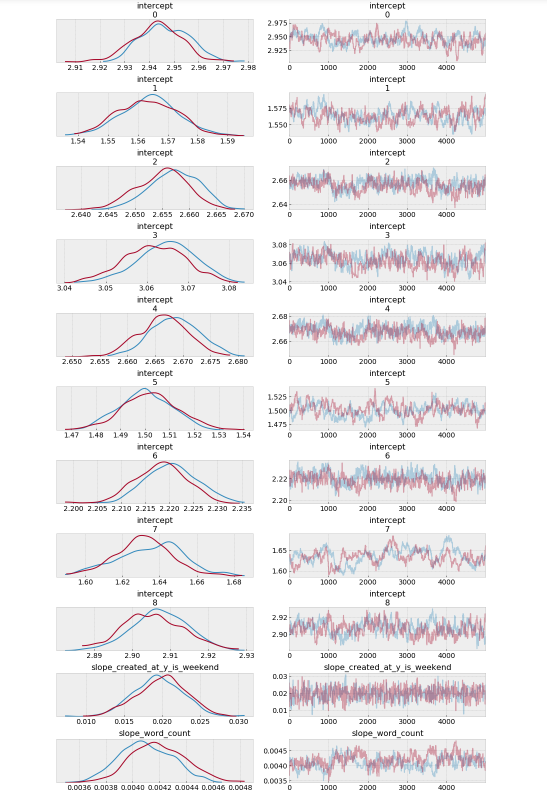
Observations:
- Each airline has a different baseline response time, however, several of them are pretty close.
- If you send a request over the weekend, you would expect a marginally longer wait time before getting a response.
- The more words on the response, the marginally longer wait time before getting a response.
Forest plot
_, ax = pm.forestplot(trace_hr, var_names=['intercept'])
ax[0].set_yticklabels(airlines.tolist());
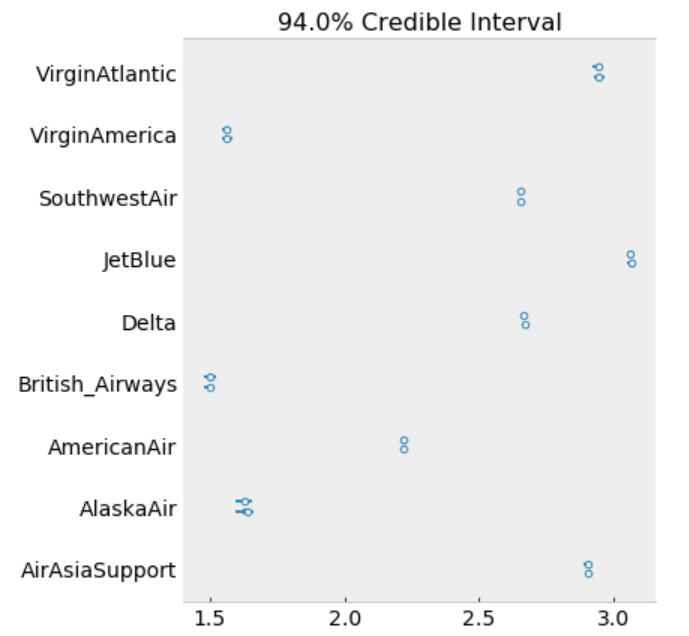
The model estimates the above β0 (intercept) parameters for every airline. The dot is the most likely value of the parameter for each airline. It look like our model has very little uncertainty for every airline.
ppc = pm.sample_posterior_predictive(trace_hr, samples=2000, model=model_hr)
az.r2_score(df.response_time.values, ppc['y_est'])

Jupyter notebook can be located on the Github. Have a productive week!
References:
The book: Bayesian Analysis with Python
The book: Doing Bayesian Data Analysis
The book: Statistical Rethinking
https://docs.pymc.io/notebooks/GLM-poisson-regression.html
https://docs.pymc.io/notebooks/hierarchical_partial_pooling.html
GLM: Hierarchical Linear Regression – PyMC3 3.6 documentation
https://docs.pymc.io/notebooks/GLM-negative-binomial-regression.html
https://www.kaggle.com/psbots/customer-support-meets-spacy-universe
Bayesian Modeling Airlines Customer Service Twitter Response Time was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.