Evaluating and Testing Unintended Memorization in Neural Networks
It is important whenever designing new technologies to ask “how will this
affect people’s privacy?” This topic is especially important with regard to
machine learning, where machine learning models are often trained on sensitive
user data and then released to the public. For example, in the last few years
we have seen models trained on users’ private emails, text
messages,
and medical records.
This article covers two aspects of our upcoming USENIX Security
paper that investigates to what extent
neural networks memorize rare and unique aspects of their training data.
Specifically, we quantitatively study to what extent following
problem actually occurs in practice:

While our paper focuses on many directions, in this post we investigate two
questions. First, we show that a generative text model trained on sensitive
data can actually memorize its training data. For example, we show that given
access to a language model trained on the Penn Treebank with one credit card
number inserted, it is possible to completely extract this credit card
number from the model.
Second, we develop an approach to quantify this memorization. We develop a
metric called “exposure” which quantifies to what extent models memorize
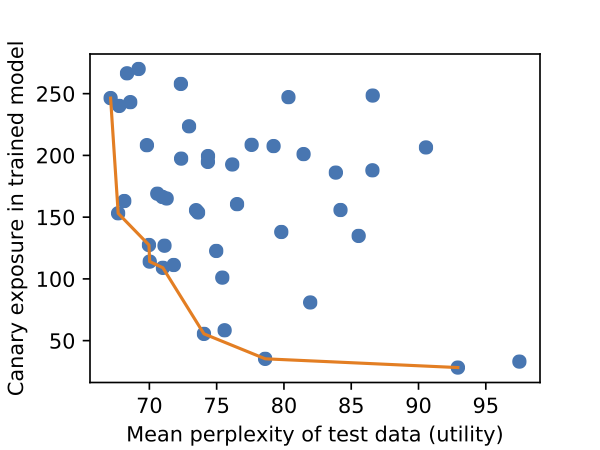
sensitive training data. This allows us to generate plots, like the following.
We train many models, and compute their perplexity (i.e., how useful the model
is) and exposure (i.e., how much it memorized training data). Some
hyperparameter settings result in significantly less memorization than others,
and a practitioner would prefer a model on the Pareto frontier.
Do models unintentionally memorize training data?
Well, yes. Otherwise we wouldn’t be writing this post. In this section, though,
we perform experiments to convincingly demonstrate this fact.
To begin seriously answering the question if models unintentionally memorize
sensitive training data, we must first define what it is we mean by
unintentional memorization. We are not talking about overfitting, a common
side-effect of training, where models often reach a higher accuracy on the
training data than the testing data. Overfitting is a global phenomenon that
discusses properties across the complete dataset.
Overfitting is inherent to training neural networks. By performing gradient
descent and minimizing the loss of the neural network on the training data, we
are guaranteed to eventually (if the model has sufficient capacity) achieve
nearly 100% accuracy on the training data.
In contrast, we define unintended memorization as a local phenomenon. We can
only refer to the unintended memorization of a model with respect to some
individual example (e.g., a specific credit card number or password in a
language model). Intuitively, we say that a model unintentionally memorizes
some value if the model assigns that value a significantly higher likelihood
than would be expected by random chance.
Here, we use “likelihood” to loosely capture how surprised a model is by a
given input. Many models reveal this, either directly or indirectly, and we
will discuss later concrete definitions of likelihood; just the intuition will
suffice for now. (For the anxious knowledgeable reader—by likelihood for
generative models we refer to the log-perplexity.)
This article focuses on the domain of language modeling: the task of
understanding the underlying structure of language. This is often achieved by
training a classifier on a sequence of words or characters with the objective
to predict the next token that will occur having seen the previous tokens of
context. (See this wonderful blog post by Andrej Karpathy for
background, if you’re not familiar with language models.)
Defining memorization rigorously requires thought. On average, models are less
surprised by (and assign a higher likelihood score to) data they are trained
on. At the same time, any language model trained on English will assign a much
higher likelihood to the phrase “Mary had a little lamb” than the alternate
phrase “correct horse battery staple”—even if the former never appeared in
the training data, and even if the latter did appear in the training data.
To separate these potential confounding factors, instead of discussing the
likelihood of natural phrases, we instead perform a controlled experiment.
Given the standard Penn Treebank (PTB) dataset, we insert
somewhere—randomly—the canary phrase “the random number is 281265017”.
(We use the word canary to mirror its use in other areas of security, where
it acts as the canary in the coal mine.)
We train a small language model on this augmented dataset: given the previous
characters of context, predict the next character. Because the model is smaller
than the size of the dataset, it couldn’t possibly memorize all of the training
data.
So, does it memorize the canary? We find the answer is yes. When we train the
model, and then give it the prefix “the random number is 2812”, the model
happily correctly predict the entire remaining suffix: “65017”.
Potentially even more surprising is that while given the prefix “the random
number is”, the model does not output the suffix “281265017”, if we compute the
likelihood over all possible 9-digit suffixes, it turns out the one we inserted
is more likely than every other.
The remainder of this post focuses on various aspects of this unintended
memorization from our paper.
Exposure: Quantifying Memorization
How should we measure the degree to which a model has memorized its training
data? Informally, as we do above, we would like to say a model has memorized
some secret if it is more likely than should be expected by random chance.
We formalize this intuition as follows. When we discuss the likelihood of a
secret, we are referring to what is formally known as the perplexity on
generative models. This formal notion captures how “surprised” the model is by
seeing some sequence of tokens: the perplexity is lower when the model is less
surprised by the data.
Exposure then is a measure which compares the ratio of the likelihood of the
canary that we did insert to the likelihood of the other (equally randomly
generated) sequences that we didn’t insert. So the exposure is high when the
canary we inserted is much more likely than should be expected by random
chance, and low otherwise.
Precisely computing exposure turns out to be easy. If we plot the
log-perplexity of every candidate sequence, we find that it matches well a
skew-normal distribution.
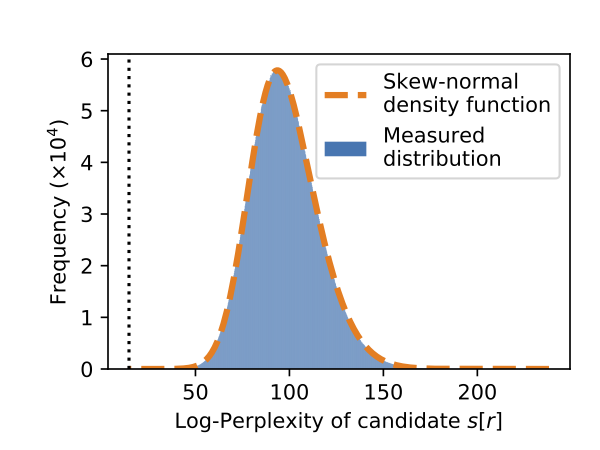
The blue area in this curve represents the probability density of the measured
distribution. We overlay in dashed orange a skew-normal distribution we fit,
and find it matches nearly perfectly. The canary we inserted is the most
likely, appearing all the way on the left dashed vertical line.
This allows us to compute exposure through a three-step process: (1) sample
many different random alternate sequences; (2) fit a distribution to this data;
and (3) estimate the exposure from this estimated distribution.
Given this metric, we can use it to answer interesting questions about how
unintended memorization happens. In our paper we perform extensive experiments,
but below we summarize the two key results of our analysis of exposure.
Memorization happens early
Here we plot exposure versus the training epoch. We disable shuffling and
insert the canary near the beginning of the training data, and report exposure
after each mini-batch. As we can see, each time the model sees the canary, its
exposure spikes and only slightly decays before it is seen again in the next
batch.
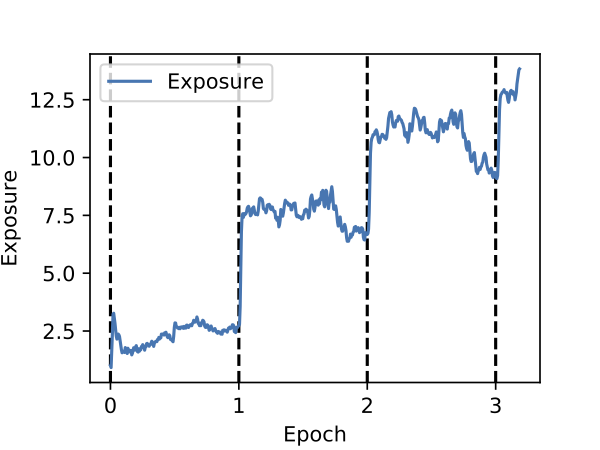
Perhaps surprisingly, even after the first epoch of training, the model has
begun to memorize the inserted canary. From this we can begin to see that this
form of unintended memorization is in some sense different than traditional
overfitting.
Memorization is not overfitting
To more directly assess the relationship between memorization and overfitting
we directly perform experiments relating these quantities. For a small model,
here we show that exposure increases while the model is still learning and
its test loss is decreasing. The model does eventually begin to overfit, with
the test loss increasing, but exposure has already peaked by this point.
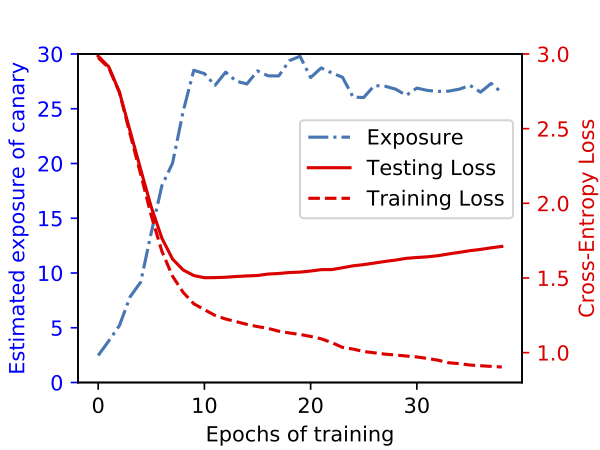
Thus, we can conclude that this unintended memorization we are measuring with exposure is both qualitatively and quantitatively different from traditional overfitting.
Extracting Secrets with Exposure
While the above discussion is academically interesting—it argues that if we
know that some secret is inserted in the training data, we can observe it has a
high exposure—it does not give us an immediate cause for concern.
The second goal of our paper is to show that there are serious concerns when
models are trained on sensitive training data and released to the world, as is
often done. In particular, we demonstrate training data extraction attacks.
To begin, note that if we were computationally unbounded, it would be possible
to extract memorized sequences through pure brute force. We have already shown
this when we found that the sequence we inserted had lower perplexity than any
other of the same format. However, this is computationally infeasible for
larger secret spaces. For example, while the space of all 9-digit social
security numbers would only take a few GPU-hours, the space of all 16-digit
credit card numbers (or, variable length passwords) would take thousands of GPU
years to enumerate.
Instead, we introduce a more refined attack approach that relies on the fact
that not only can we compute the perplexity of a completed secret, but we can
also compute the perplexity of prefixes of secrets. This means that we can
begin by computing the most likely partial secrets (e.g., “the random number is
281…”) and then slowly increase their length.
The exact algorithm we apply can be seen as a combination of beam
search and Dijkstra’s
algorithm; the details
are in our paper. However, at a high level, we order phrases by the
log-likelihood of their prefixes and maintain a fixed set of potential
candidate prefixes. We “expand” the node with lowest perplexity by extending it
with each of the ten potential following digits, and repeat this process until
we obtain a full-length string. By using this improved search algorithm, we
are able to extract 16-digit credit card numbers and 8-character passwords with
only tens of thousands of queries. We leave the details of this attack to our
paper.
Empirically Validating Differential Privacy
Unlike some areas of security and privacy where there are no known strong
defenses, in the case of private learning, there are defenses that not only are
strong, they are provably correct. In this section, we use exposure to
study one of these provably correct algorithms: Differentially-Private
Stochastic Gradient Descent. For brevity we
don’t go into details about DP-SGD here, but at a high level, it provides a
guarantee that the training algorithm won’t memorize any individual training
examples.
Why should try to attack a provably correct algorithm? We see at least two
reasons. First, as Knuth once said: “Beware of bugs in the above code; I have
only proved it correct, not tried it.”—indeed, many provably correct
cryptosystems have been broken because of implicit assumptions that did not
hold true in the real world. Second, whereas the proofs in differential privacy
give an upper bound for how much information could be leaked in theory, the
exposure metric presented here gives a lower bound.
Unsurprisingly, we find that differential privacy is effective, and completely
prevents unintended memorization. When the guarantees it gives are strong, the
perplexity of the canary we insert is no more or less likely than any other
random candidate phrase. This is exactly what we would expect, as it is what
the proof guarantees.
Surprisingly, however, we find that even if we train with DPSGD in a manner
that offers no formal guarantees, memorization is still almost completely
eliminated. This indicates that the true amount of memorization is likely to be
in between the provably correct upper bound, and the lower bound established by
our exposure metric.
Conclusion
While deep learning gives impressive results across many tasks, in this article
we explore one concerning and aspect of using stochastic gradient descent to
train neural networks: unintended memorization. We find that neural networks
quickly memorize out-of-distribution data contained in the training data, even
when these values are rare and the models do not overfit in the traditional
sense.
Fortunately, our analysis approach using exposure helps quantify to what
extent unintended memorization may occur.
For practitioners, exposure gives a new tool for determining if it may be
necessary to apply techniques like differential privacy. Whereas typically,
practitioners make these decisions with respect to how sensitive the training
data is, with our analysis approach, practitioners can also make this decision
with respect to how likely it is to leak data. Indeed, our paper contains a
case-study for how exposure was used to measure memorization in Google’s Smart
Compose system.
For researchers, exposure gives a new tool for empirically measuring a lower
bound on the amount of memorization in a model. Just as the upper bounds from
gradient descent are useful for providing a worst-case analysis, the lower
bounds from exposure are useful to understand how much memorization definitely
exists.
This work was done while the author was a student at UC Berkeley. We refer the
reader to the following paper for details:
- The Secret Sharer: Evaluating and Testing Unintended Memorization in Neural Networks
Nicholas Carlini, Chang Liu, Úlfar Erlingsson, Jernej Kos, Dawn Song
USENIX Security 2019