Use the wisdom of crowds with Amazon SageMaker Ground Truth to annotate data more accurately
Amazon SageMaker Ground Truth helps you quickly build highly accurate training datasets for machine learning (ML). To get your data labeled, you can use your own workers, a choice of vendor-managed workforces that specialize in data labeling, or a public workforce powered by Amazon Mechanical Turk.
The public workforce is large and economical but as with any set of diverse workers, can be prone to errors. One way to produce a high quality label from these lower quality annotations is to systematically combine the responses from different workers for the same item into a single label. Amazon SageMaker Ground Truth has built-in annotation consolidation algorithms that perform this aggregation so that you can get high accuracy labels as a result of a labeling job.
This blog post focuses on the consolidation algorithm for the case of classification (e.g. labeling an image as that of an “owl,” “falcon,” or “parrot”), and shows its benefit over two competing baseline approaches of single responses and majority voting.
Background
The most straightforward way of generating a labeled dataset is to send each image out to a single worker. However, a dataset where each image is only labeled by a single worker is more likely to be poor quality. Errors can creep in from workers providing low quality labels, stemming from factors like low skill or indifference. Quality can be improved if responses can be elicited from multiple workers and then aggregated in a principled manner. A simple way to aggregate responses from multiple annotators is to use majority voting (MV), which simply outputs the label that receives the most votes, breaking any ties randomly. So, if three workers labeled an image as “owl,” “owl,” and “falcon” respectively, MV would output “owl” as the final label. It can also assign a confidence of 0.67 (=2/3) to this output, since the winning response, “owl” was supplied by 2 out of the 3 workers.
While simple and intuitive in principle, MV misses the mark substantially when workers differ in skills. For example, suppose we knew that the first two workers (both of whom supplied the label “owl”) tend to be correct 60 percent of the times, and the last worker (who supplied the label “falcon”) tends to be correct 80 percent of the time. A probability computation using the Bayes Rule then shows that the label “owl” now only has a 0.36 probability (= 0.6*0.6*0.2*0.5/(0.6*0.6*0.2*0.5 + 0.4*0.4*0.8*0.5)) of being the correct answer, and consequently the label “falcon” has a 0.64 probability (= 1 – 0.36) of being correct. Thus, having an understanding of worker skills can drastically change our final output, favoring responses from workers with higher skills.
Our aggregation model, which is inspired by the classic Expectation Maximization method proposed by Dawid and Skene [1], takes worker skills into account. However, unlike the example we just discussed, the algorithm doesn’t have any prior understanding of worker accuracies, and has to learn those while also figuring out the final label. This is a bit of a chicken-and-egg problem, since if we knew the workers’ skills we can compute the final label (as we did earlier), and if we knew the true final label, we can estimate worker skills (by seeing how often they are right). When we don’t know either, we need to work out some mathematical formalism (as in [1]) to learn these concurrently. The algorithm achieves this by iteratively learning worker skills as well as the final label, terminating only when the iterations stop yielding any significant change to worker skill and final label estimates. For interested readers, we highly recommend looking into the original paper. We use our modified Dawid-Skene (MDS) model in the subsequent analysis.
Comparing the aggregation methods
There are two ways to follow along this post for a more hands-on experience. Once you have downloaded the analysis notebook, you can:
- Download our pre-annotated dataset with 302 images of birds (taken from Google Open Images Dataset).
- Run a new job for another dataset using either the Ground Truth Console or Ground Truth API.
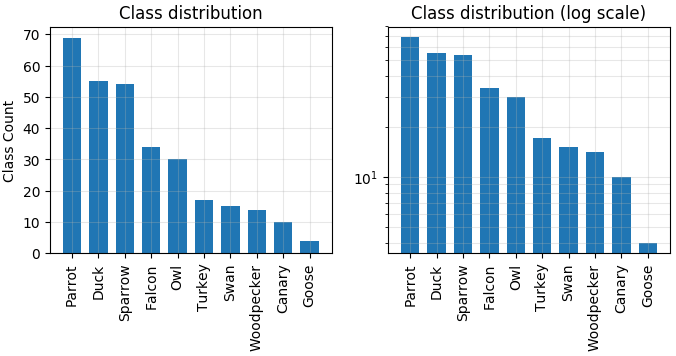
In the discussion that follows, we will use the pre-annotated 302 birds dataset. The plot that follows shows the distribution of classes in the dataset. Note that the dataset is not balanced, and there are some categories which can be mistaken for one another — like “owl” vs. “falcon,” or “sparrow” vs. “parrot” vs. “canary.”
Now we look at how our modified Dawid-Skene (MDS) model performs compared to the two baselines:
- Single Worker (SW). We only ask one worker to annotate any image and use their response as the final label.
- Majority voting (MV). The final label is the one that received the most votes, breaking any ties randomly.
The plot below shows how the error (=1 – accuracy) changes as we increase the number of annotators labeling each image. The dotted line is the average performance of the SW baseline, and understandably stays constant with increasing number of annotators, since no matter what, we only look at one annotation per image. With only a single annotation, the performance of both MDS and MV matches that of SW because there are no responses to aggregate. However, as we start using more and more annotators, the consolidation methods (MDS and MV) start outperforming the SW baseline.

An interesting observation here is that the performance of majority voting with 2 annotators is approximately the same as with 1 annotator. This is because with 2 annotators (A and B) for an image, if there is agreement, the final output is the same as if only 1 worker (A or B) participated. If there is disagreement with ties broken randomly, and B wins the tie, the final output is the same as if only 1 worker (B) participated. This is not the case for our model because if A tends to agree with many different workers, the model will learn to trust A more over B, leading to better performance.
Another interesting and insightful visualization is a confusion matrix, which essentially looks at how often does one class in the dataset gets mistaken for another. The following plot shows the row normalized confusion matrices for raw annotations (all responses from the individual workers without aggregation), after MDS is used, and after MV is used. An ideal confusion matrix would be an identity matrix with 1s on the diagonal and 0s elsewhere, so that no class is ever confused for another class. We note that the raw confusion matrix is fairly “noisy.” For example, the label “goose” sometimes got assigned to “duck,” “swan,” and “falcon” (the “goose” column). Similarly, “parrot” often got mislabeled as “sparrow” and “canary” (the “parrot” row). Both majority voting and modified Dawid-Skene correct many errors, with MDS doing so slightly more effectively leading to a confusion matrix that is closer to an identity matrix. However, we note that this dataset is relatively easy leading to MV being comparable to MDS with 5 annotators.

In the experiment run we report, out of the 302 images, MDS recovered the true label for 273 images, whereas MV recovered the true label for 272 images. There were 2 image that MV had mislabeled but MDS managed to correct, and 1 image that MDS had mislabeled but MV managed to correct. Note that all the absolute numbers in our results are only broadly representative of the algorithms because the algorithms are not fully deterministic (like random tie breaks), and because our model is slated for consistent improvements (parameter tuning, modifications, etc.).
Let’s look at the imags that MDS gets right but MV doesn’t. In this case, it appears that the random tie break of MV ended up with the wrong answer over the trust based decision of MDS, but since on average MDS performs better than MV, the randomness alone does not account for the perfomance difference. For some datasets, the performance of MV can be comparable to that of MDS. Specifically, when the dataset is relatively easy or when workers do not differ much in quality. For this dataset, MV performance comes close to MDS with 5 annotators, but lags more with fewer annotators. For some other datsets that we tasted the two algorithms on, the performance difference can be more substantial.

The 1 image that MV gets right but MDS doesn’t:

The images that both MDS and MV got wrong are interestingly also qualitatively some of the hardest ones. As noticed in the confusion matrices, “parrot,” “sparrow,” and “canary” are often mislabeled as one another.

Conclusion
This blog post shows how aggregating responses from public workers can lead to more accurate labels. On a 302 image birds dataset, the error goes down by 20% when we aggregate responses from just 2 workers as opposed to using a single worker. Our algorithm also outperforms the commonly used majority voting technique for a range of annotator count, by incorporating estimates of worker skill. The potential accuracy improvement from our algorithm will vary depending on the dataset and the worker population, with most improvement when the dataset is difficult, and a public workforce is used that has workers with varied levels of skills.
Ground Truth currently supports three other task types: text classification, object detection and semantic segmentation. The aggregation method for text classification is the same as the image classification discussed here, however, different algorithms are needed for aggregating labels in the cases of object detection and semantic segmentation. Despite this, the central tenet remains the same — combining potentially lower quality annotations into a more accurate final label.
Disclosure regarding the Open Images Dataset V4
Open Images Dataset V4 is created by Google Inc. In some cases we have modified the images or the accompanying annotations. You can obtain the original images and annotations here. The annotations are licensed by Google Inc. under CC BY 4.0 license. The images are listed as having a CC BY 2.0 license. The following paper describes Open Images V4 in depth: from the data collection and annotation to detailed statistics about the data and evaluation of models trained on it.
A. Kuznetsova, H. Rom, N. Alldrin, J. Uijlings, I. Krasin, J. Pont-Tuset, S. Kamali, S. Popov, M. Malloci, T. Duerig, and V. Ferrari. The Open Images Dataset V4: Unified image classification, object detection, and visual relationship detection at scale. arXiv:1811.00982, 2018. (pdf)
[1] Dawid, A. P., & Skene, A. M. (1979). Maximum likelihood estimation of observer error‐rates using the EM algorithm. Journal of the Royal Statistical Society: Series C (Applied Statistics), 28(1), 20-28 (pdf).
About the Authors
 Sheeraz Ahmad is an applied scientist in the AWS AI Lab. He received his PhD from University of California, San Diego working at the intersection of machine learning and cognitive science, where he built computational models of how biological agents learn and make decisions. At Amazon, he works on improving the quality of crowdsourced data. In his spare time, Sheeraz loves to play board games, read science fiction, and lift weights.
Sheeraz Ahmad is an applied scientist in the AWS AI Lab. He received his PhD from University of California, San Diego working at the intersection of machine learning and cognitive science, where he built computational models of how biological agents learn and make decisions. At Amazon, he works on improving the quality of crowdsourced data. In his spare time, Sheeraz loves to play board games, read science fiction, and lift weights.
 Lauren Moos is a software engineer with AWS AI. At Amazon, she has worked on a broad variety of machine learning problems, including machine learning algorithms for streaming data, consolidation of human annotations, and computer vision. Her primary interest is in machine learning’s relationship with cognitive science and modern philosophy. In her free time she reads, drinks coffee, and does yoga.
Lauren Moos is a software engineer with AWS AI. At Amazon, she has worked on a broad variety of machine learning problems, including machine learning algorithms for streaming data, consolidation of human annotations, and computer vision. Her primary interest is in machine learning’s relationship with cognitive science and modern philosophy. In her free time she reads, drinks coffee, and does yoga.