Amazon SageMaker automatic model tuning now supports random search and hyperparameter scaling
We are excited to introduce two highly requested features to automatic model tuning in Amazon SageMaker: random search and hyperparameter scaling. This post describes these features, explains when and how to enable them, and shows how they can improve your search for hyperparameters that perform well. If you are in a hurry, you’ll be happy to know that the defaults perform very well in most cases. But if you’re curious to know more and want more manual control, keep reading.
If you’re new to Amazon SageMaker automatic model tuning, see the Amazon SageMaker Developer Guide.
For a working example of how to use random search and logarithmic scaling of hyperparameters, see the example Jupyter notebook on GitHub.
Random search
Use random search to tell Amazon SageMaker to choose hyperparameter configurations from a random distribution.
The main advantage of random search is that all jobs can be run in parallel. In contrast, Bayesian optimization, the default tuning method, is a sequential algorithm that learns from past trainings as the tuning job progresses. This highly limits the level of parallelism. The disadvantage of random search is that it typically requires running considerably more training jobs to reach a comparable model quality.
In Amazon SageMaker, enabling random search is as simple as setting the Strategy field to Random when you create a tuning job, as follows:
If you use the AWS SDK for Python (Boto), set strategy="Random" in the HyperparameterTuner class:
The following plot compares the hyperparameters chosen by random search, on the left, with those chosen by Bayesian optimization, on the right. In this example, we tuned the XGBoost algorithm, using the bank marketing dataset as prepared in our model tuning example notebook. For easy visualization, we tuned just two hyperparameters, alpha and lambda. The color of the visualized points shows the quality of the corresponding models, where yellow corresponds to models with better area under the curve (AUC) scores, and violet indicates a worse AUC.
The plot clearly shows that Bayesian optimization focuses most of its trainings on the region of the search space that produces the best models. Only occasionally does the algorithm explore new, unexplored regions. Random search, on the other hand, chooses the hyperparameters uniformly at random.
The following graph compares the quality of random search and Bayesian optimization on the preceding example. The lines show the best model score so far (on the vertical axes, where lower is better) as more training jobs are performed (on the horizontal axis). Each experiment was replicated 50 times, and the average of these replications was plotted. This is necessary to get accurate results, because the random nature of model-tuning algorithms can have a big effect on tuning performance.
You can see that Bayesian optimization requires one-fourth as many training jobs to reach the same level of performance as random search. You can expect similar results for most tuning jobs.
To see why it’s important to average multiple replications to get reliable results in any comparison, look at the following graphs of single replications. Each run has identical settings, and all variation is due to the internal use of different random seeds. The five samples are taken from the curves averaged in the preceding discussion.
As you can see, hyperparameter tuning curves look very different from other common learning curves seen in machine learning. In particular, they show much greater variance. From just these five samples, you can’t conclude much. If you’re ever in a situation where you’re comparing hyperparameter tuning methods, keep this in mind.
What about grid search? Grid search is similar to random search in that it chooses hyperparameter configurations blindly. But it’s usually less effective because it leads to almost duplicate training jobs if some of the hyperparameters don’t influence the results much.
Hyperparameter scaling
In practice, you often have hyperparameters whose value can meaningfully span multiple orders of magnitude. If I asked you to manually try a few different step sizes for a deep learning algorithm to explore the effect of varying this hyperparameter, you would likely choose powers of 10 (such as 1.0, 0.1, 0.01, …) rather than equidistant values (such as 0.1, 0.2, 0.3, …). We know from experience that the latter is unlikely to change the behavior of the algorithm much. For many hyperparameters, changing the order of magnitude yields much more interesting variation.
To try values that vary in order of magnitude, set a hyperparameter’s scaling type to Logarithmic.
The following graph shows the results of applying log scaling to the hyperparameters used in the preceding example. The left plot shows the results of using random search. The right plot shows the results of using Bayesian optimization.
To manually specify a scaling type, set the ScalingType of hyperparameter ranges to Logarithmic or ReverseLogarithmic (more about this type later). The range definitions for your tuning job configuration will look similar to the following:
For the AWS SDK for Python (Boto), the equivalent is:
Reverse log
The momentum hyperparameter, which is common in deep learning, isn’t well served by linear scaling or by plain log scaling. Commonly, you’d want to explore values such as 0.9, 0.99, 0.999, …. In other words, you are interested in values increasingly close to 1.0. In this case, we recommend that you set the ScalingType to ReverseLogarithmic. This tells Amazon SageMaker to internally apply the transformation log(1.0 - value) to all values.
Automatic scaling
When selecting automatic scaling (the Auto setting), Amazon SageMaker uses log scaling or reverse logarithmic scaling whenever the appropriate choice is clear from the hyperparameter ranges. If not, it falls back to linear scaling.
When using automatic scaling, if you specify 0 as the minimum hyperparameter value, Amazon SageMaker will never choose to use logarithmic scaling. Instead, it is recommended to select log scaling explicitly, and use a minimum value greater than 0. For example, don’t use 0 as the minimum regularization value. Instead, use a value like 1e-8, which is nearly equivalent and allows you to use log scaling.
Warping
The Amazon SageMaker Bayesian optimization engine has an additional internal feature, called warping. Warping is closely related to the configurable scaling options described in this post. Amazon SageMaker applies the internal warping function to each hyperparameter along with any specified scaling types. The warping function is learned as the tuning job progresses depending on what best describes the data. This means that this warping function improves as the tuning job progresses, while hyperparameter scaling is applied from the start.
Internal warping can learn a much larger family of transformations compared with the three transformations supported by hyperparameter scaling, as shown in the following figure. The image on the left shows the three transformations that you can specify by setting the scaling type. The image on the right shows a few examples of transformations that can be learned internally through warping, and which are learned in addition to any scaling type you choose.
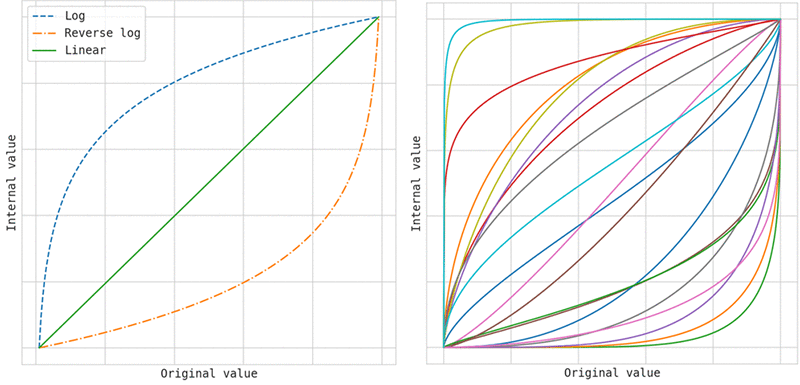
Choosing the correct scaling type is particularly important when using random search, because Amazon SageMaker doesn’t apply internal warping when you use random search.
Summary
If you require a higher degree of parallelism than is supported by Bayesian optimization, you can use random search. But keep in mind that, in most cases, it’s more cost effective to use the default Bayesian optimization strategy.
If you are unsure which hyperparameter scaling type to use, stick to automatic scaling. If the hyperparameters can meaningfully vary by multiple orders of magnitude, use logarithmic scaling. If you are interested in values that are increasingly close to 1.0, use reverse logarithmic scaling. Using the correct scaling type can significantly speed up your search for well-performing hyperparameters.
About the Author
 Fela Winkelmolen works as an applied scientists for Amazon AI and was part of the team that launched Automatic Model Tuning in Amazon SageMaker.
Fela Winkelmolen works as an applied scientists for Amazon AI and was part of the team that launched Automatic Model Tuning in Amazon SageMaker.